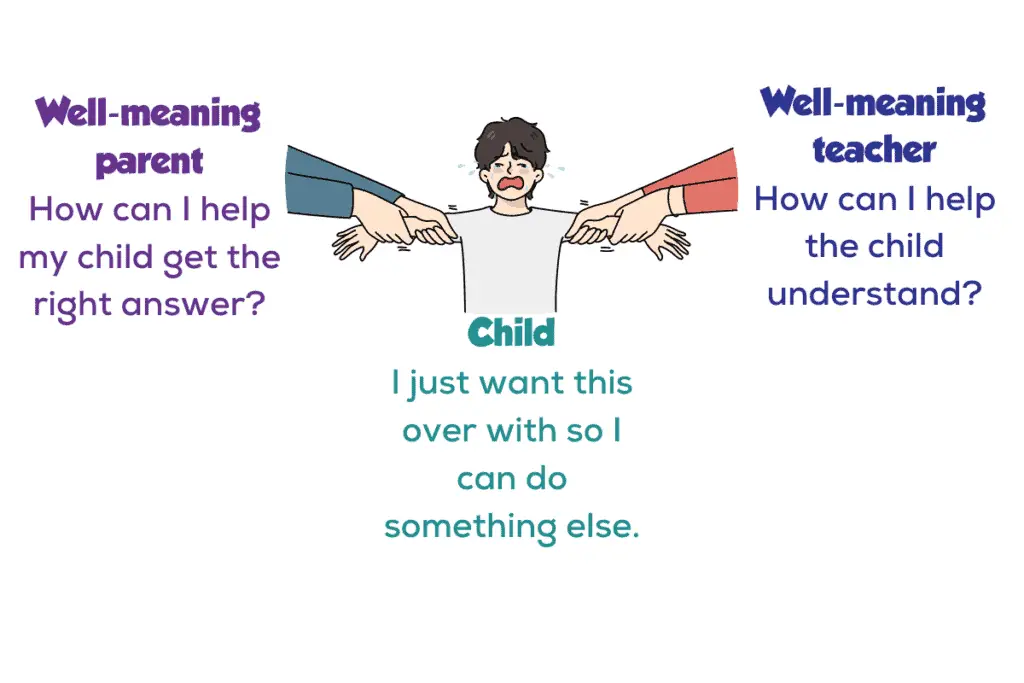
I recently asked teachers what parents do that undermines their efforts to teach children math. Two main themes emerged: The damage of shortcutting mathematical practices and the language of negative mindsets. This post addresses the shortcuts, tricks, and algorithms well-meaning parents teach their children at home. Future posts will address parents’ negative math language as well as how parents can approach these tasks instead.
What shouldn’t parents do? (Part 1)
Parents should avoid teaching tricks and algorithms that they learned unless it is the method the student is learning in class.
This post contains affiliate links. If you purchase through these links, I may earn a small commission at no additional cost to you. You can read more about how I choose affiliates and products at my affiliate page.
Tricks and algorithms undermine understanding
As a kid watching my teacher’s head explode, I can tell you that my well-meaning father teaching me the English way to do the math because it made it easier for him to help me with my homework…not so helpful.
Letty, on a break from teaching to raise her children
In the past, computing power was not what it is now. Humans needed quick, efficient methods to compute. (Think, for example, of the stories represented in the movie Hidden Figures.) Even after calculators and computers became common, math instruction still relied heavily on teaching the old “quick, efficient computation” methods. However, teaching and learning practice has finally caught up to the technological age. We recognize now how important it is to teach the concepts underlying math structure, and that a focus on the computation methods has undermined student understanding of structure. Your child is probably bringing home methods that focus more on numeracy and conceptual understanding, rather than speed and efficiency. If you struggle with these methods, know that you were likely trained under a fully different (and, frankly, outdated) philosophy of math learning, where “right” and “fast” were prioritized over understanding.
What undermines your math teaching?
Mandy, a District Math Coach
“Teaching tricks/short-cuts/algorithms when we are working to build conceptual understanding.”
Even further back, resources such as paper were expensive and hard to come by. So those “quick, efficient” methods of accurately computing needed also to be efficient in space. This led to all sorts of shortcut notations (such as “carrying the one”) that saved space, but also gave teachers and students a way out of understanding why it was happening, since all they had to learn was when and how to do it. Can you fully explain to an 8-year-old why we “carry” or “borrow”? (If not, check out my blog post on this.) Even for those of us who can, the understanding came long after we learned how.
What undermines your math teaching?
Tara, a High School Math Teacher
“Teaching ‘tricks’ to memorize that undercut the conceptual understanding”
“’That’s not how I learned it.’”
Education is supposed to be (in my opinion) about passing down the knowledge of our species in as efficient and meaningful a way as possible, so that we don’t all have to reinvent and rediscover that knowledge on our own, and so that we can communicate with each other and make decisions based on the full knowledge of our species in addition to our own experiences. There is an overdue shift now toward making math instruction meaningful in the technological age. When we carry in our pockets machines that can do the complicated computations, it’s more important that we understand when and why the different types of computations are needed and how to check that the machines are performing as we need them to.
When we carry in our pockets machines that can do the complicated computations, it’s more important that we understand when and why the different types of computations are needed and how to check that the machines are performing as we need them to.
Math Teacher Barbie
In the Western world at least, we have a history of teaching and learning mathematics in a vacuum, without its historical and social contexts. Some even believe math exists without historical and social contexts. But every human endeavor exists within history and society. In the ongoing debate about whether math was invented or discovered, I propose that math was neither invented nor discovered. Instead, math was, and continues to be, articulated. By this, I mean that the math we choose to observe and teach are
- paid attention to because of what the observer finds necessary, important, or interesting
- put into language developed within societies and groups of people, thus
- limited to the language and needs/interests of those observing the patterns.
So let’s use modern needs to determine how to teach math, and let’s use language to articulate it in a way that expresses the underlying structures and eases students’ paths to deeper understanding all through their math learning career. (For an example of this change of language, check out this blog post on regrouping.)
Regardless of whether I’ve convinced you or you’re still skeptical, I encourage you to try not to teach shortcuts, tricks, and algorithms before their time. Your child will be taught the traditional algorithms, and may even be taught a few tricks and shortcuts, in good time. However, we know from many years of experience that teaching these algorithms too early undermines the important conceptual understanding and ideas. Those algorithms that have served us so well to get to this point in history will not be forgotten and will be passed down. But right now, we need students who understand why they work, not just how to do them.
As always, model for your children what you desire for them. Keep your chin high, persist, and remember that
You’ve Got This!

