(Click aqui para leer este articulo en español.)

Word problems are the bane of math students’ existence. Sometimes we could easily solve the exact same problem if it came up in real life but struggle when presented as a word problem. Perhaps it’s the phrasing, the reading, or simply the fear of getting it wrong. Most likely, the reason is different for everyone.
Many step-by-step word-problem strategies have been proposed, and your child may even be learning one of them in class. Part of those strategies are lists of “translations” from words into operations, i.e., a list of “key” or “clue” words for each operation. All of these, though, can fail us at one time or another. So how do we reliably know whether to add, subtract, multiply, or divide in a word problem?
To determine which operation to use in a word problem, look at the relationship between the different quantities. Typically, addition or subtraction is best with groups of different sizes. Choose multiplication or division when the groups are all the same size or when scaling (making something bigger or smaller without changing its overall look or proportions).
Addition or subtraction is useful when two or more of the quantities can be counted or combined together to make one greater group. This is also known as a part-part-whole relationship (or part-part-part-whole, etc.) Multiplication or division is useful when there are a number of equal-sized groups either being combined or split apart. These can be combined together for more complicated relationships (such as counting a certain number of groups of one quantity and then addition an additional amount on top of that).
This post was originally published on mathteacherbarbie.com. If you are viewing it elsewhere, you are viewing a stolen copy.
Start by ignoring the numbers
Seriously! Ignore the numbers. Read the problem out loud. Instead of reading a number, use the word “some” or similar word. Do you have two or more groups being combined together to create another group (addition), or a subgroup being taken out of a larger group (subtraction)? Are you scaling something up or down or making some number of copies of a group (multiplication), or splitting a quantity up into equal smaller groups (division)?
Prewrite the answer
Focus on what the problem is asking you to find. Reword the question or statement into a complete sentence answer, leaving the numbers blank (if it helps, put in the word “some” where a number might go). Not only will this give you a great setup when you get to the end of the problem, but it can be extremely helpful in helping you figure out the context of the problem.
Most real world problems start question-first (I need to know ____, or I wonder ___), and we have to go find the information to answer. We’re often pretty good at this. Word problems in math class tend to give us the information first, then the question. This may be part of what becomes overwhelming. Turn that back around and focus first on the goal, and you may suddenly find you have a lot more insight than you thought.
Use simpler numbers to figure out relationships
As you begin to understand the context, start bringing the numbers back in. If the numbers are large, fractions, or decimals, consider temporarily pretending that the numbers are much smaller. Read the problem, but substitute whole numbers, the kind of number that might be Sesame Street’s Number of the Day, just until you figure out what operations and relationships exist. (Then make sure to remember to put the original numbers back into place!)
Decide what kinds of relationships your quantities have
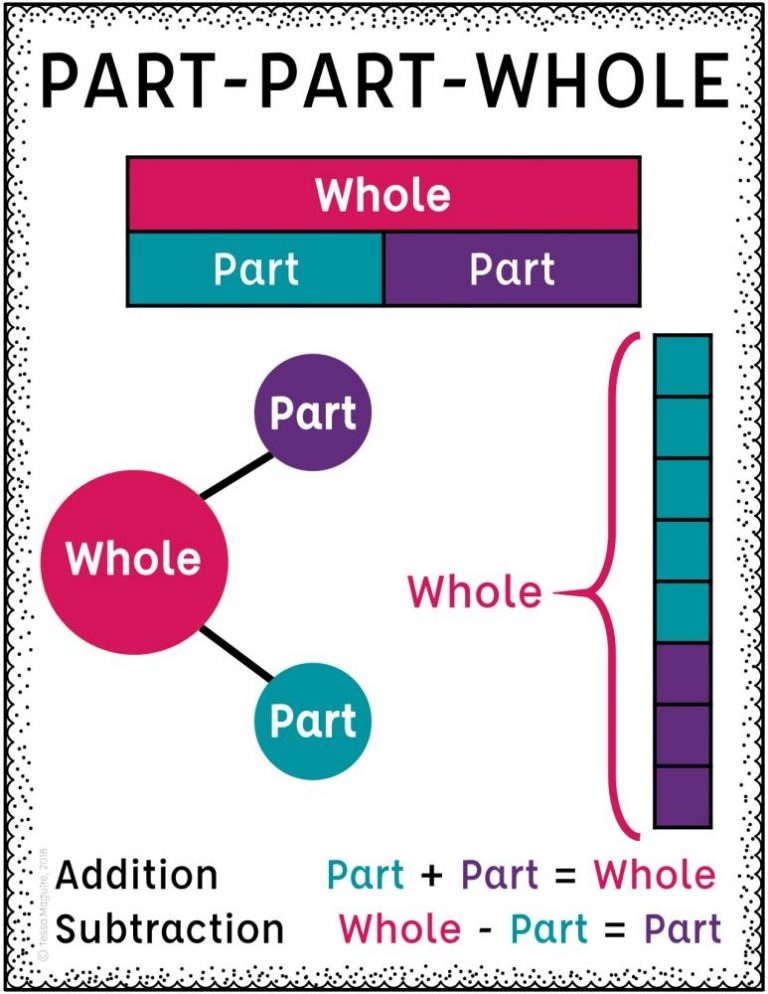
If you go through the steps above and still don’t see the relationships, consider the following:
- Addition: If you have more than one part making up a whole, and you want to know about the whole, you’re likely in an addition scenario. Elementary curricula are often calling this a part-part-whole relationship. All of the addition “key words” indicate this type of relationship:
- total or sum of the parts
- one part more than or increased by another part
- all the parts together, in all, combined
- etc.
- Subtraction: Subtraction also involves a part-part-whole relationship, but this time you want to find out about one of the parts.
- how many were in the part that you took away; how many more than the remaining part did you used to have
- what’s the difference between the whole and the remaining part
- how many less than do you have in the remaining part than was in the total
- Multiplication: Multiplication may be repeated groups of equal size or scaling up (numbers bigger than one) or down (fractions between 0 and 1) proportionally.
- Division: Division also deals with repeated groups of equal size or scaling. However, division answers either the number of groups or the size of each group (whereas multiplication answers the total of all the groups). While you can use division for scaling up or down, once you learn to use fractions, it is often easier to think of all scaling as multiplication.
Many word problem strategies teach primarily lists of “key words” such as the ones in italics above. There are three problems with relying on this strategy:
- Keyword lists are really hard to memorize.
- No keyword list is complete.
- Several keywords (such as more than) appear on multiple lists!
This is why focusing on the relationships between quantities is more reliable than key word lists.
Combine operations as needed
If you see more than one of these types of relationships, you might need to use more than one operation! For example, you may have one part of a part-part-whole that is itself made up of same-sized groups, which would mean combining addition and multiplication. Or you may find that some portion was taken away, with the remaining part being split into equal groups: subtraction and division! Take the focus away from the numbers, look for the relationships among the nouns in the problem, not the quantities, and choose your operations with confidence and with a whole lot less guessing.
You’ve Got This!
