The area model is a tool for organizing multiplication and division problems. The area model helps to ensure that each place value of one factor (one of the numbers being multiplied) is appropriately multiplied by each place value once and only once of the other factor (we call this the distributive property of multiplication). If we multiplied in a disorganized manner, it would be difficult to keep track. The area model helps by organizing the information in a visual, geometric way. The area model is especially useful in extending itself to multiply numbers other than integers (such as fractions and decimals) as well as multiplying and factoring polynomials in algebra. Few multiplication models and algorithms are as versatile as the area model.
It’s important to note, though, that no model, not even the area model, can overcome weak knowledge of basic multiplication facts and addition skills! Keep practicing those basic facts however and as often as you can until they area second nature. My post How to Learn Multiplication Facts gives a few ideas how to do this.
This post was originally published on mathteacherbarbie.com. If you are reading it anywhere else, you are viewing a stolen version.
What Is an Area Model?
An area model represents multiplication (and its opposite — division) as the area of a rectangle with given side lengths. You might remember that the area of a rectangle is computed as length $\times$ width. This forms the basis of the area model. For a deeper dive into this basic definition of the area model and why it works, check out What Does an Area Model Represent? or either of my videos What Is the Area Model? and Why Does the Area Model Work?.
To begin, think about a bunch of little squares, all the same size.

If I wanted to use the area model to multiply $4 \times 7$, I would start a rectangle by lining up four squares along one side and seven squares along another:
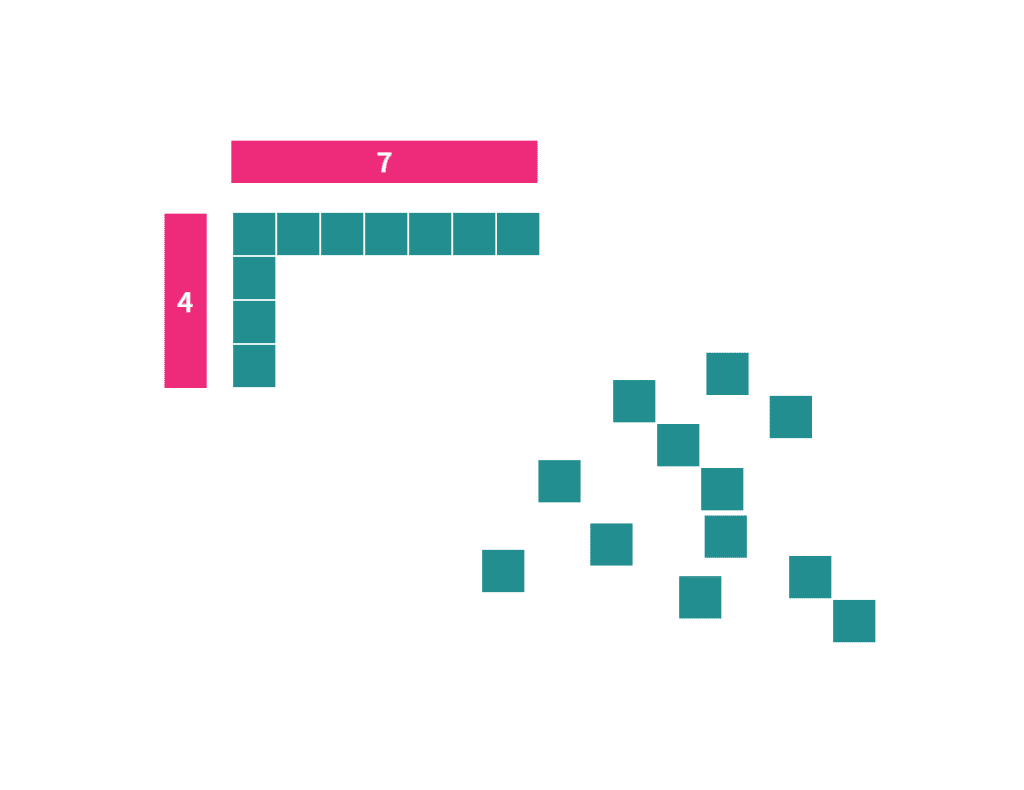
Can you picture the implied rectangle shape? Does your image match the rectangle below?
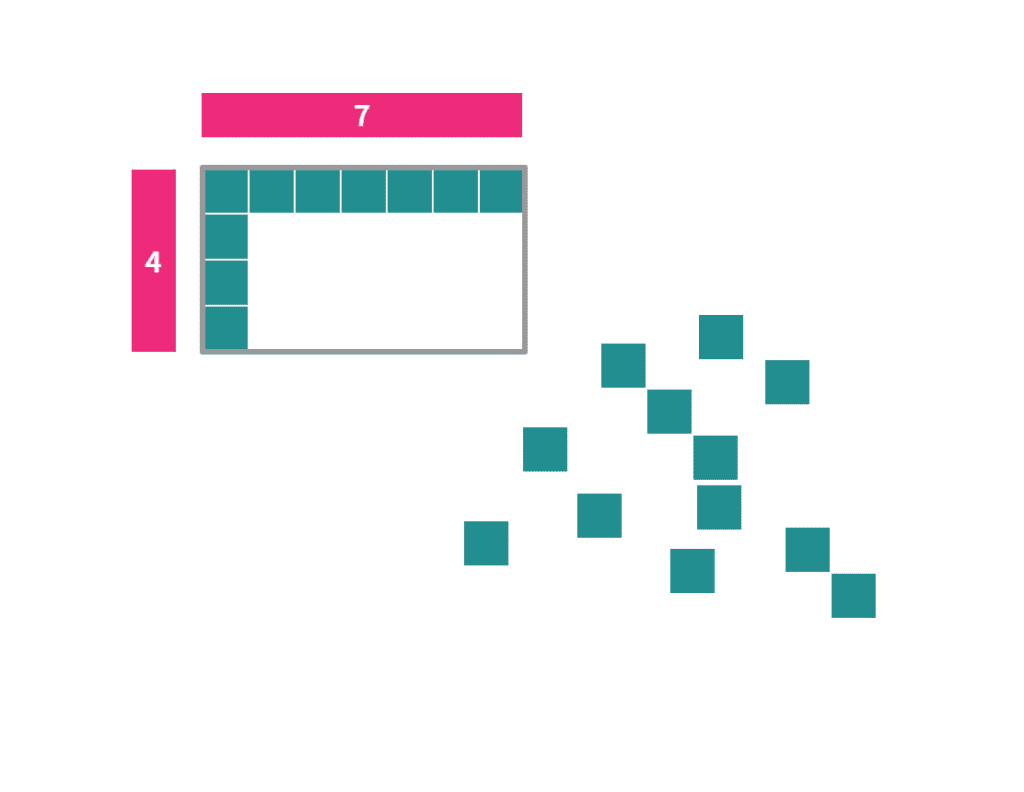
The number of those little squares that it takes to perfectly fill that rectangle is what we call the area of the rectangle. (And the units of that area are square units because they’re little 2-dimensional (length x width) squares making it up!)
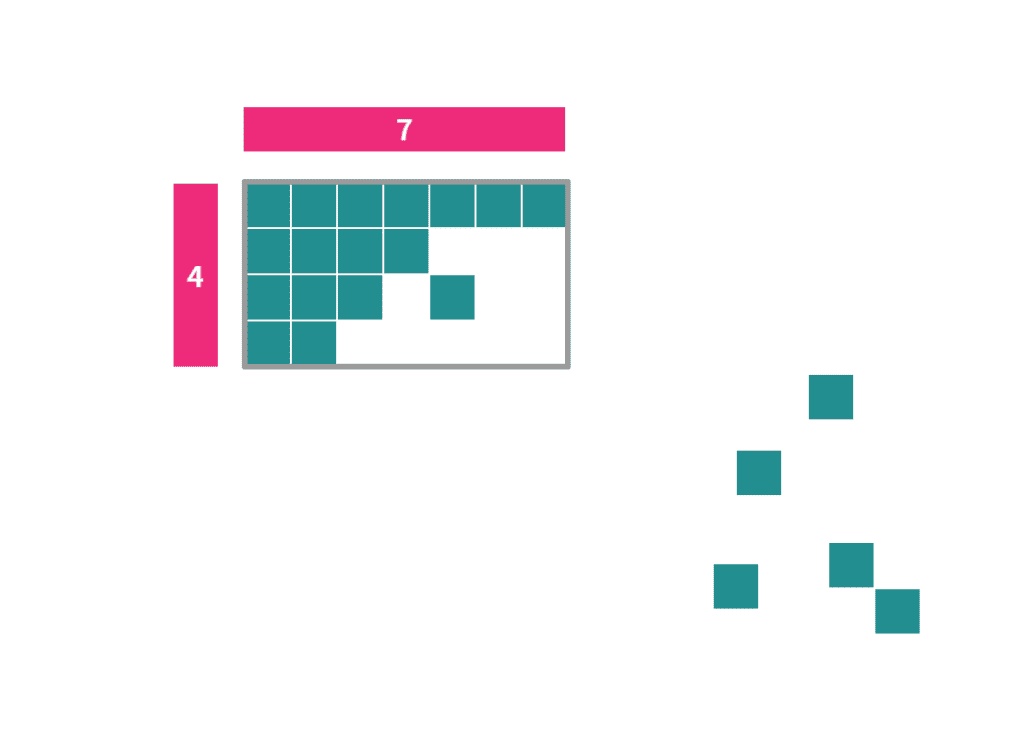
Image created in Polypad by Mathigon.org
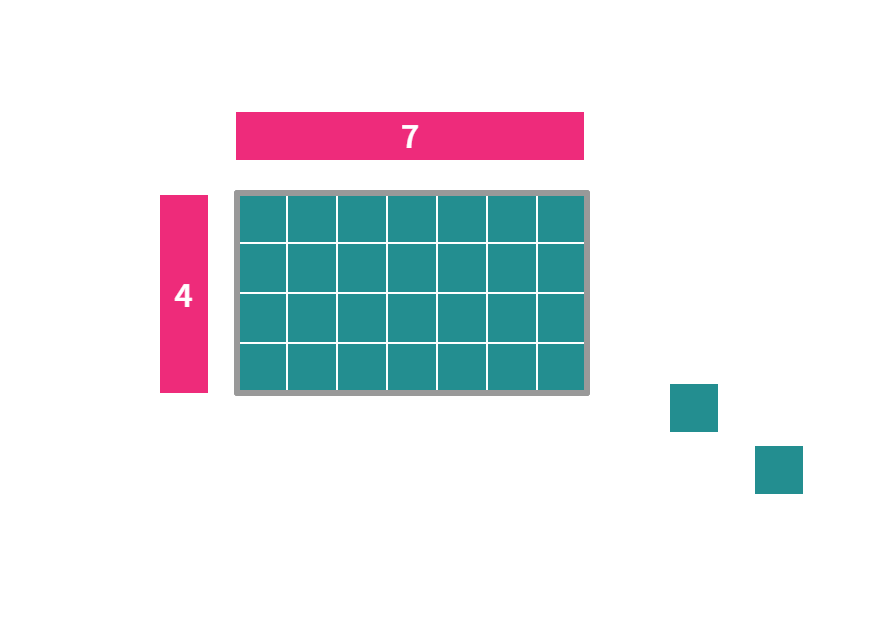
Image created in Polypad by Mathigon.org
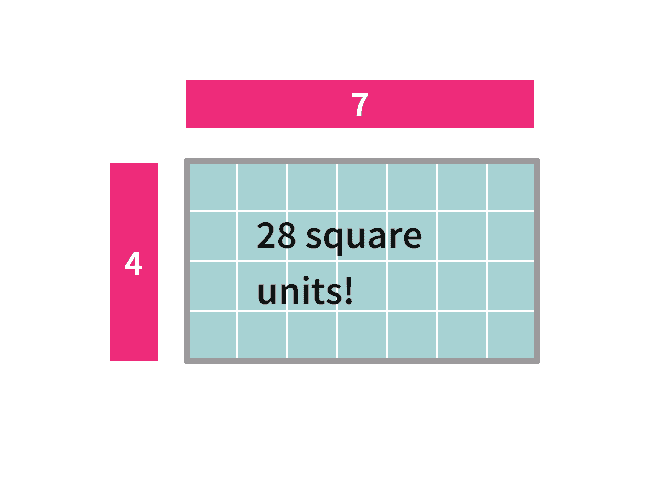
Because we were able to pack exactly 28 of the little squares into this rectangle, we now know that $4 \times 7=28$.
This is the basis of the area model. However, it’s a bit much to move these squares around all the time. Who wants to sit and literally count them when the numbers get big?! (I’d lose count if I tried. Would you?) So let’s see if we can write this more simply, building on this basic idea but without having to show every little detail, only the most important bits.
Area model multiplication
Before we completely let go of the little squares, let’s look at one more multiplication problem. Hopefully you remember from memorizing your multiplication tables that $12 \times 12=144$. Let’s see how we might set that up in the area model. We’ll look side-by-side at how we can model it the same way as before, as well as how we can make it abstract (and simpler to use).
We start the same way as before: by setting up a rectangle that is 12 units wide by 12 units tall:
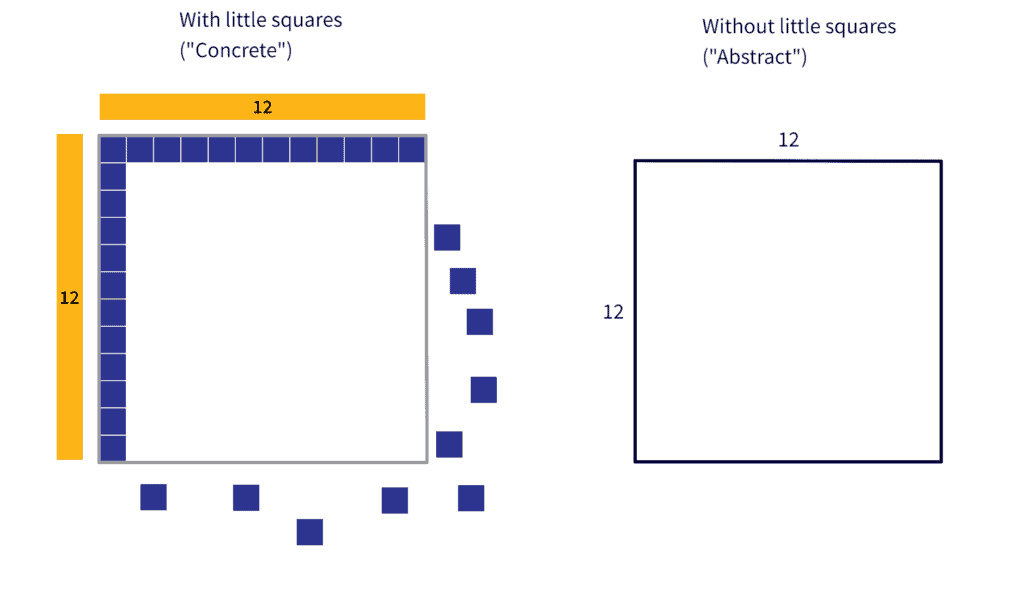
Key to moving from the concrete to the abstract, and from small numbers to larger numbers, in this model is noticing that 12 can be broken up into its component place values: $12=10+2$.
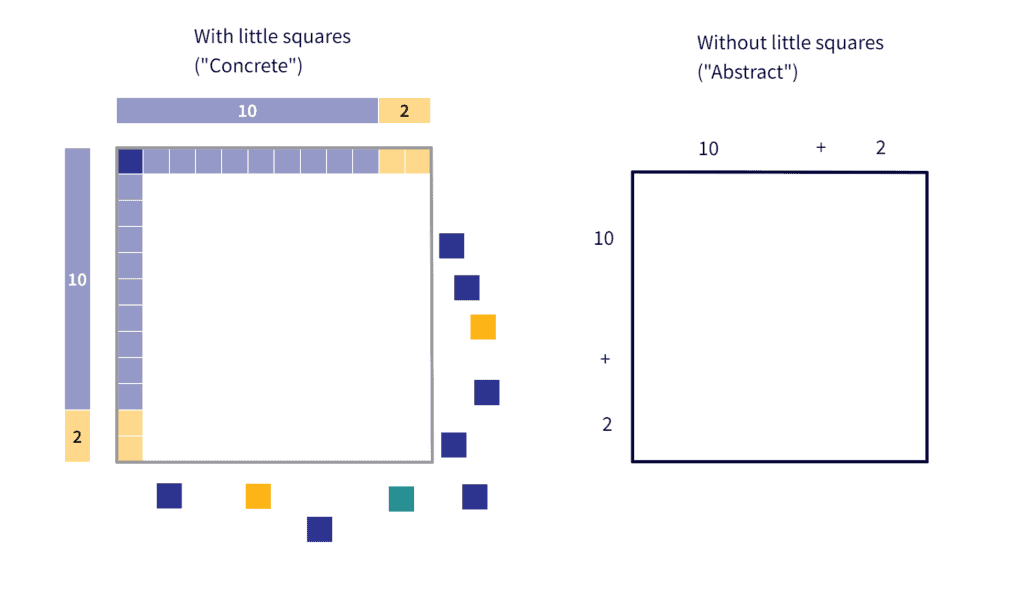
Breaking the $12$ into $10+2$ allows us to split the square up into smaller rectangles. While this might seem like more work at the moment, what it allows us to do is to create much easier multiplication problems that we can do in our heads once we have the multiplication tables memorized:
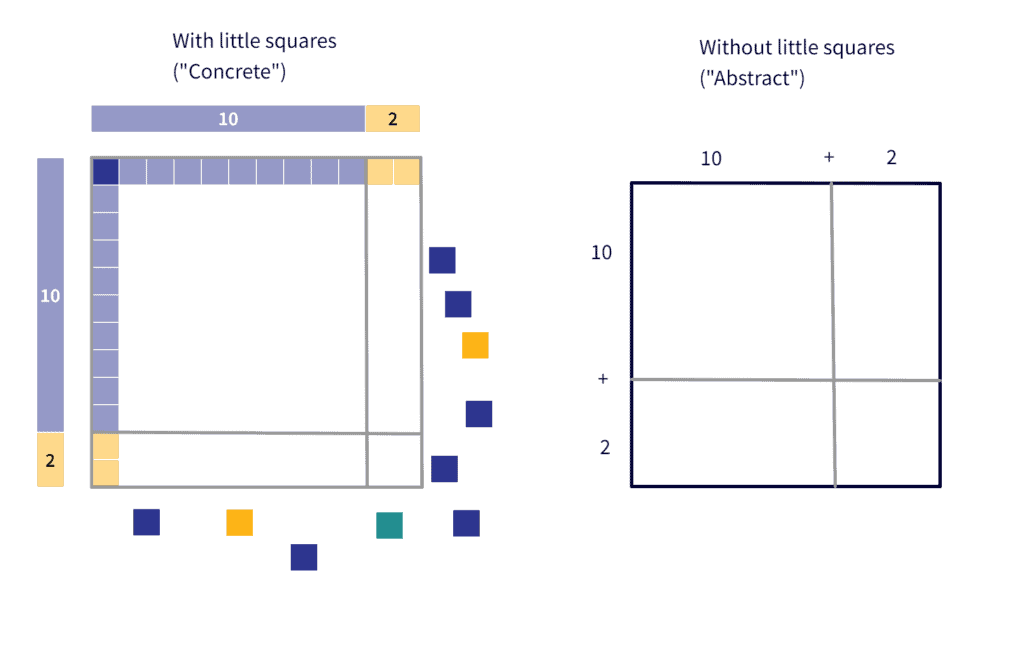
Image created in Polypad by Mathigon.org
Now we fill in each smaller (internal) rectangle with the appropriate number of little squares (concrete), or we do each simpler multiplication problem (abstract), and then in the final step, we’ll be able to add all those little areas to find the bigger area, but one step at a time.
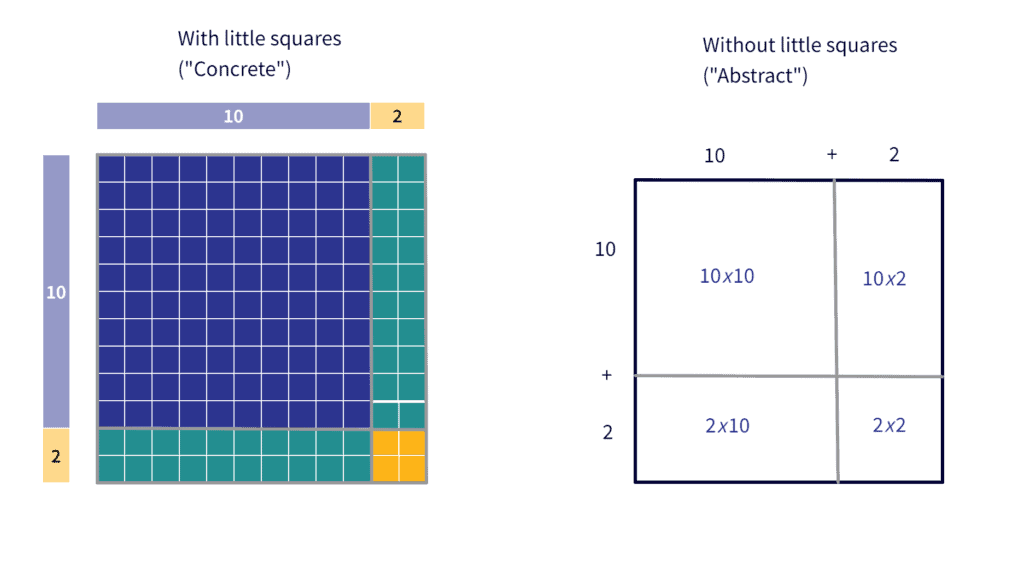
So how much area does this bigger square (the twelve-by-twelve square that represents $12 \times 12$) cover?
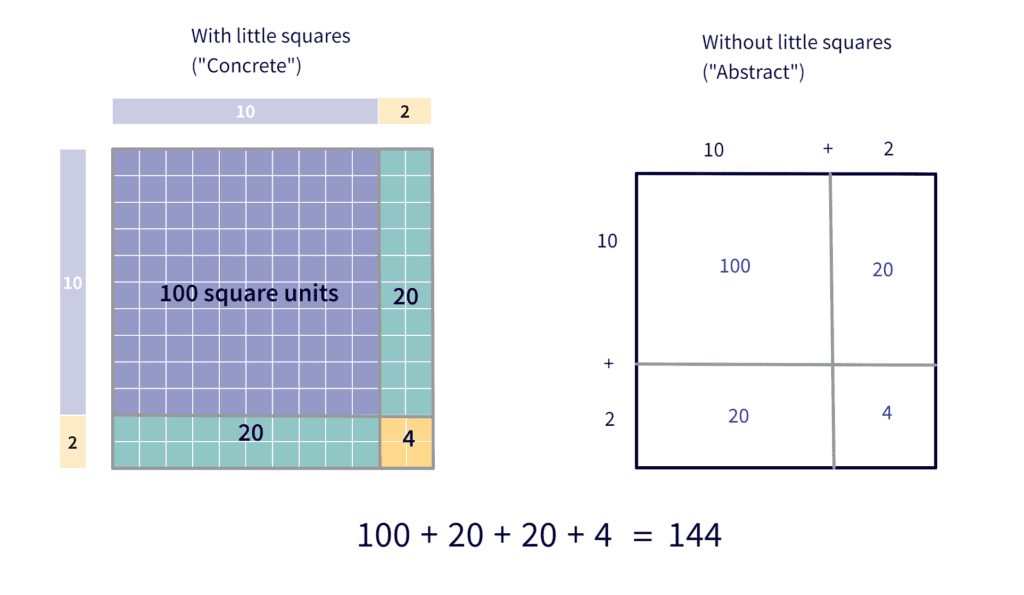
$12 \times 12 = 100+20+20+4=144$
The area model really shines when we multiply a 3-digit number by a 2-digit number, such as $729 \times 42$.
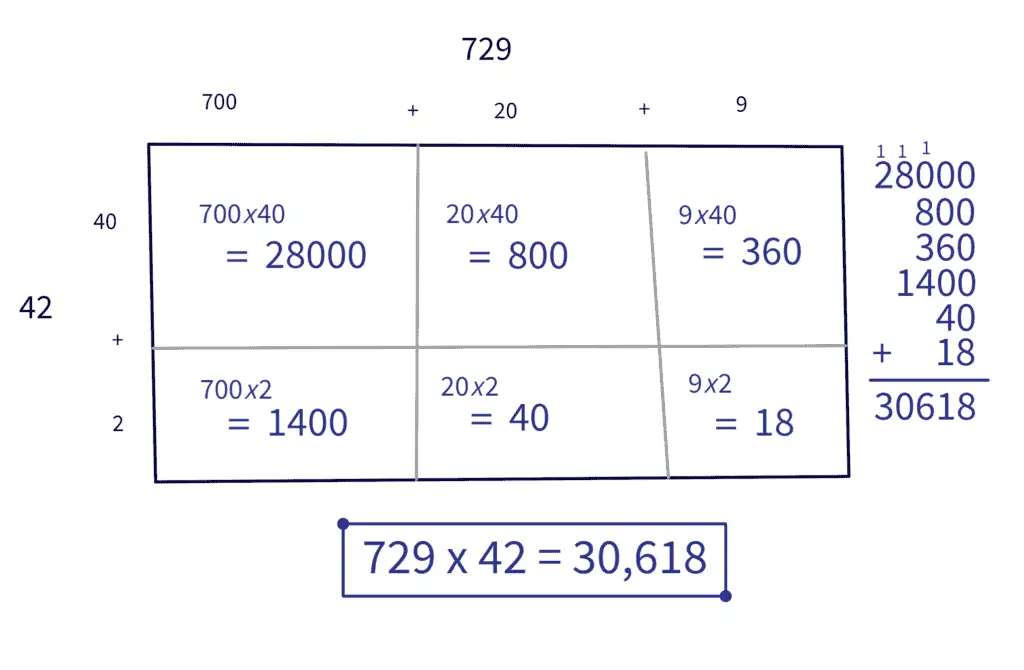
For more detail and more examples of multiplying using the area model, check out Multiplying with the Area Model (blog post) and/or Using the Area Model to Multiply Larger Numbers (video).
Area model division
Division is the inverse operation of multiplication. In other words, we can think of it as multiplication’s opposite or a way of undoing multiplication or unmultiplying. It flips multiplication around, giving us the product (or the result of the related multiplication fact, known as the dividend in division) and one of the factors of the related multiplication fact (known as the divisor in division). A division problem asks us to find the other factor of the related multiplication problem (known as the quotient in division.).
In other words, our setup for a division area model problem has us looking for one of the sides of the rectangle, not the area.
If we wanted to compute $30618 \div 42$, we would set up our rectangle with $30618$ inside representing the total area and $42$ along the left-hand side representing the height. Then we would will look for the width of the rectangle to answer the problem.

Image created in Polypad by Mathigon.org
Area model multiplication (discussed above) starts by splitting the sides into their component place values. In contrast, area model division relies on splitting the total area into blocks whose size are multiples of the divisor (the number being divided by). We then use each of those blocks to determine the unknown side (the quotient or answer to the division question).
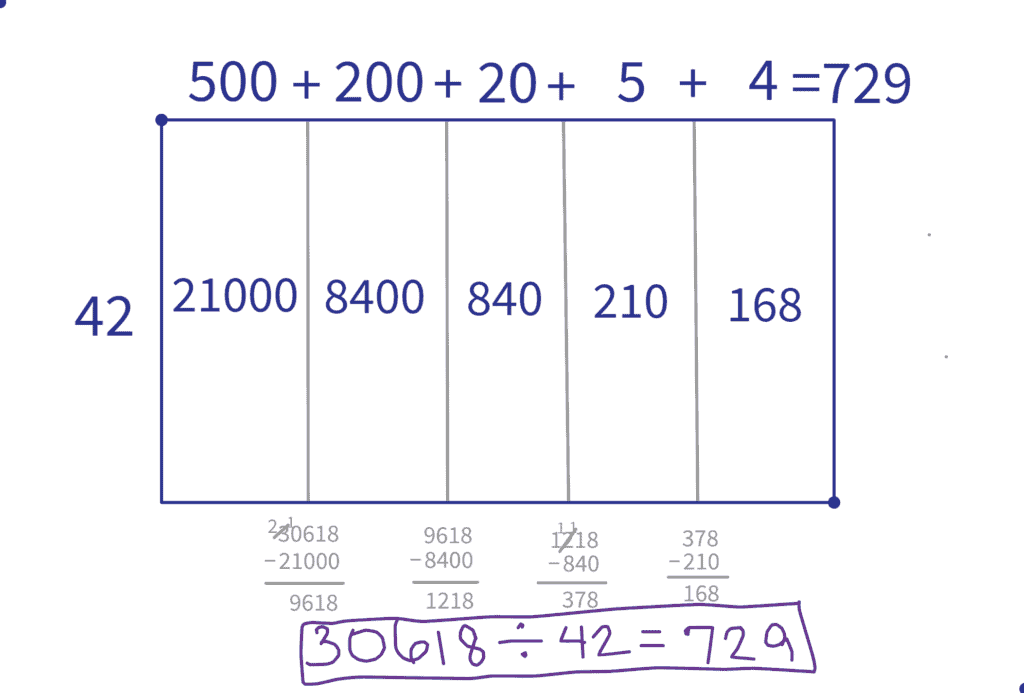
Image created in Polypad by Mathigon.org
To see $30618 \div 42$ worked out step-by-step using the area model, see my post Dividing with the Area Model.
When the area model is a good choice
The area model’s strengths shine in multiplication particularly, and when the factors (numbers being multiplied together) have 2 or 3 digits each. However, the area model does work with any number of digits. It can, however, become unwieldy and overwhelming with too many, and is not always the most efficient with too few.
With appropriate discussion, the area model can help emphasize and teach the need to distribute every digit of one number by every digit of the other number exactly and only once. It is, in essence, an organizational tool to make this happen. Most other algorithms (both western-style school algorithms and a myriad others found online) are also simply organizational tools. However, the area model is a visualization accessible to many in ways that some of the other algorithms aren’t. It can help students become familiar with that process that I call double-distributing (not an official math term, but maybe it will catch on some day) before seeing it in less visual algorithms.
The area model is a great tool to connect arithmetic to geometry. Because some cultures throughout history (the Ancient Greeks come to mind, but there were others) generally thought about all math in terms of geometry, the area model also connects us to mathematical history and heritage in various ways.
The area model also works as a bridge to multiplying fractions, decimals, and polynomials. It extends easily into these realms, as we’ll see below, and provides consistency and familiarity for students facing what can otherwise seem scary-new.
When other methods are better
When one of the factors being multiplied is a single-digit, either memory-based or algorithm-based models of solving might be easier. For example, nothing beats the speed of knowing one’s multiplication table when the problem is $12 \times 12$ or smaller. And when the problem is beyond the times table, the area model comes down to a simple expansion and distributing, which is easily done without the framework of the boxes:
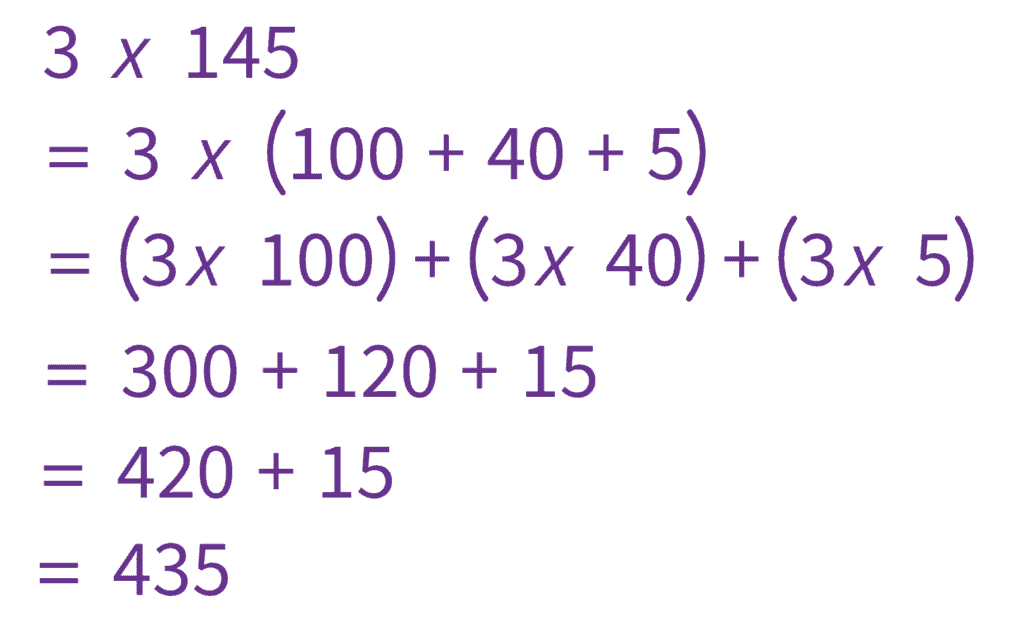
When the factors (numbers being multiplied together) are larger than 3 digits, the area model can be visually overwhelming and lend less advantage in calculations. It was never the most efficient model, but at larger and larger numbers, its becomes less and less efficient. So despite its visual, intuitive nature, the overwhelm of those visuals and the loss of efficiency often leave it a poor choice for numbers in the thousands and greater.
Though useful in division, the area model’s strength really is in multiplication (with the possible exception of factoring in algebra). Some students and teachers may find the visual nature of the area model useful in division, and others may not find it any more intuitive than other division models.
Extending the area model to other number types
One huge advantage of the area model is how it extends to other number types and even into algebra. Students who are fluent with the area model can use it to ease a familiar path into these new concepts and begin to make sense of them.
Multiplying fractions with the area model
The area model is useful at multiple stages of multiplying fractions. Using simple boxes with sides of unit 1 and simple proper fractions, the area model can be used to help derive or prove the process of multiplying fractions as that of multiplying the numerators and multiplying the denominators straight across:
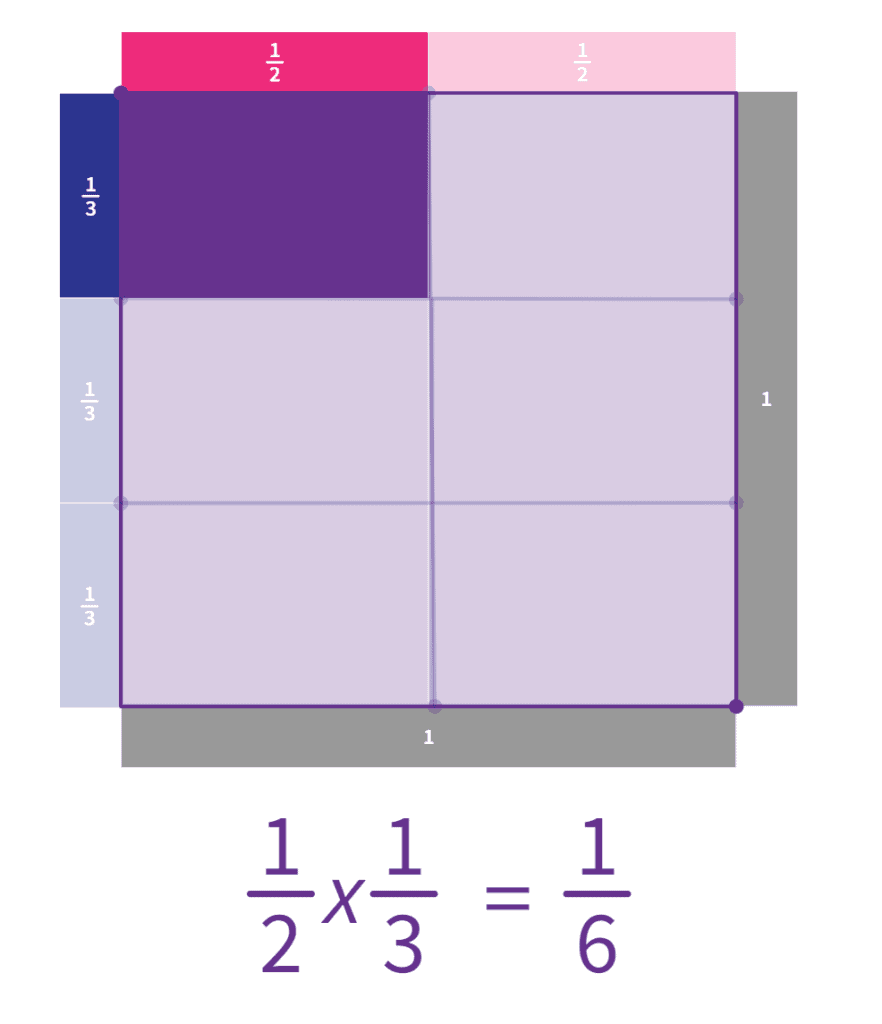
Image created in Polypad by Mathigon.org
To multiply mixed numbers, students area almost always taught that they must change the mixed number to an improper fraction before multiplying. In order to use the “multiply-straight-across” mentality, this is absolutely true. However, mixed numbers can be multiplied as mixed numbers if one remembers to “double-distribute” (my term, not an official math term). The area model provides us a way of seeing, doing, and organizing that process of multiplying mixed numbers as mixed numbers.
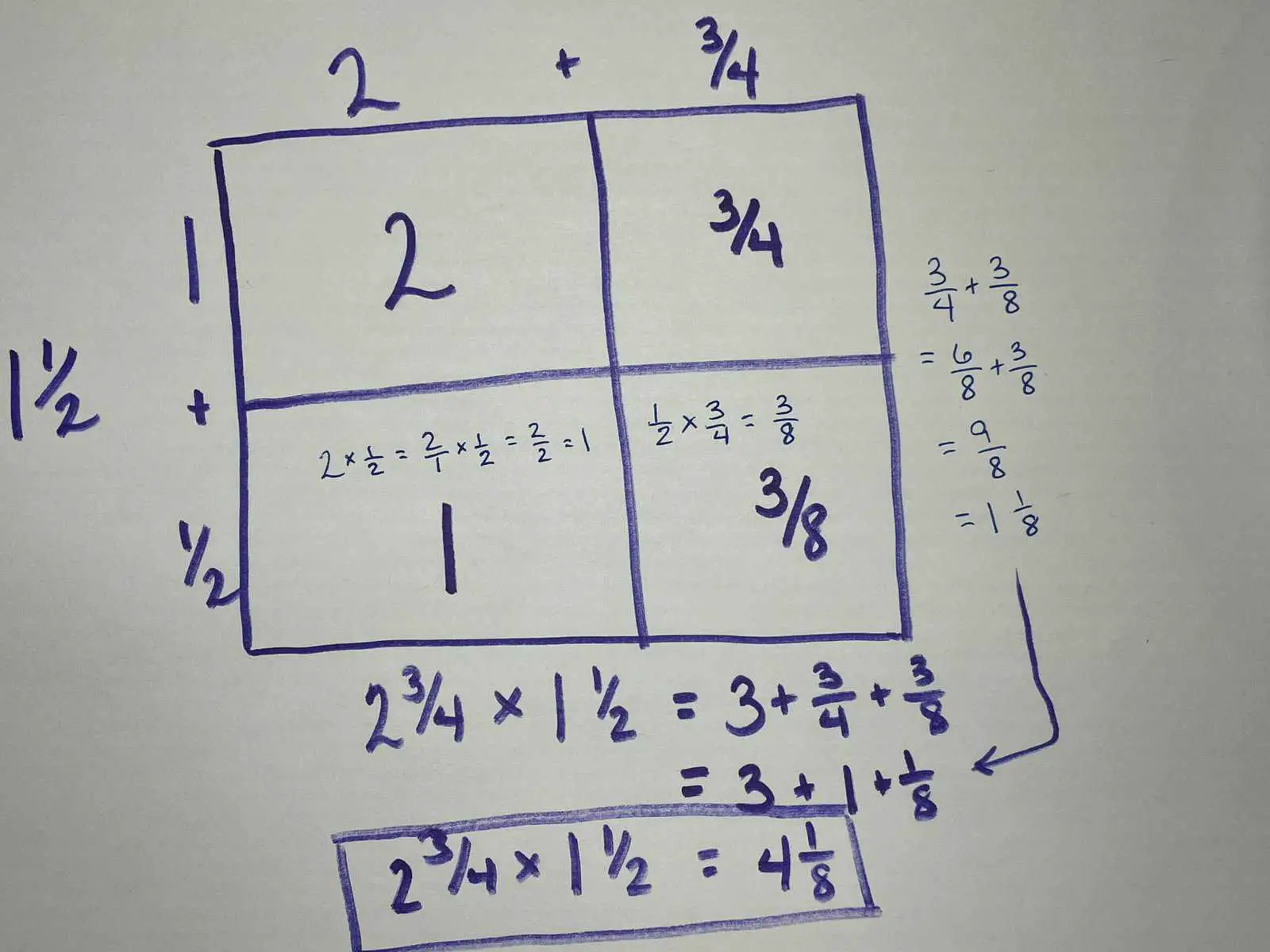
Multiplying decimals with the area model
Because the area model is simply a way of organizing place value and the distributive property, it works just as well for multiplying decimals as other numbers. Some basic instruction is needed first about what happens when place values to the right of the decimal point are multiplied, before jumping in feet first. (Just like knowing how to multiply by 10 and the zeros as placeholders in multi-digit number expansions was necessary before using the area model to multiply larger numbers.) However, using the area model to multiply fractions of $\frac{1}{10}$, $\frac{1}{100}$, and moving between the fractions and decimal forms can greatly aid even this step of the process.
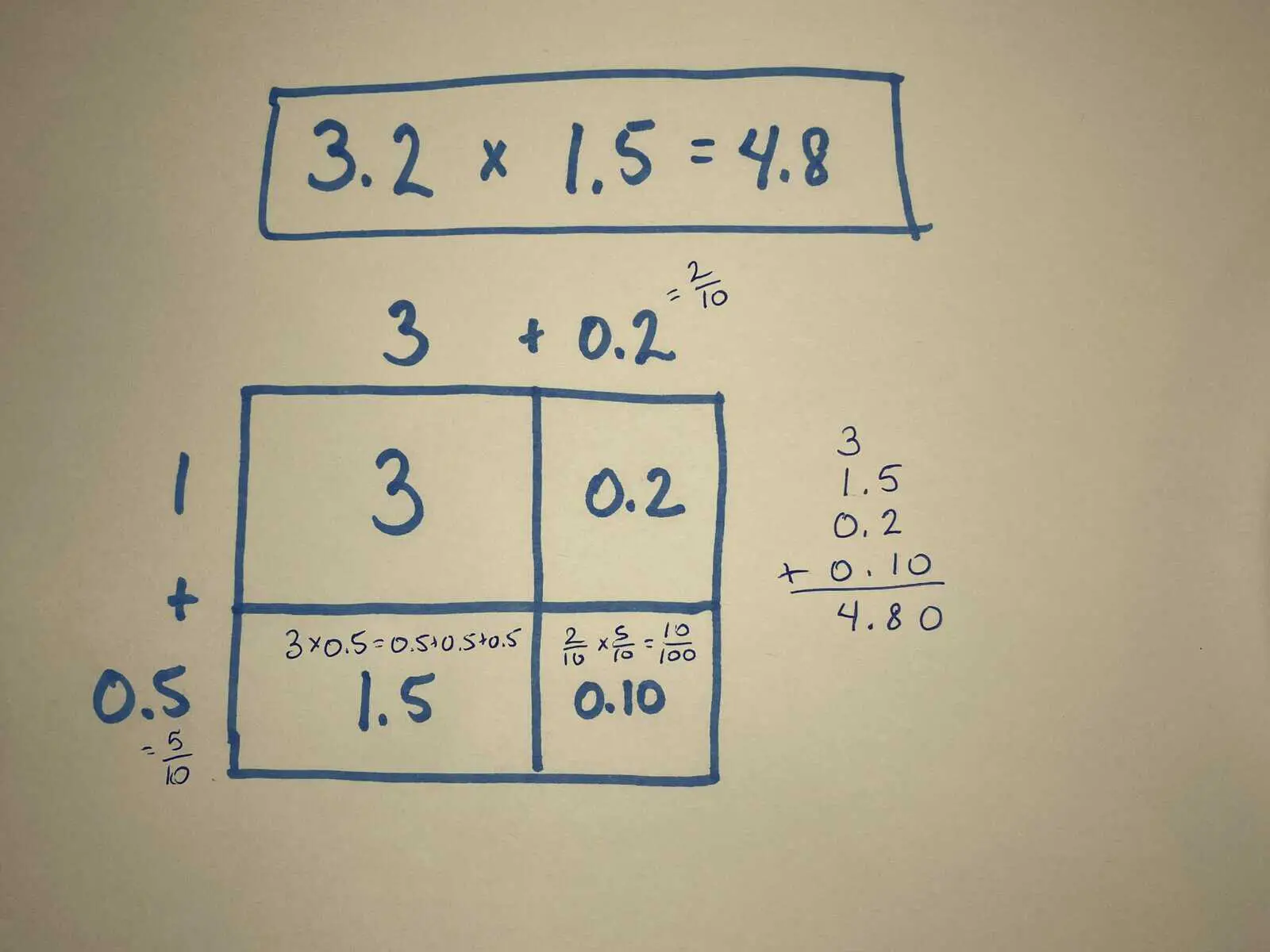
Extending the area model into algebra
I know when I learned algebra, I struggled to see what other mathematicians saw as the connections between polynomials and our base-10 number system. My breakthrough moment came when I started using the area model more and more in algebra. Turns out: each term in a polynomial corresponds to a place value in the base-10 number! In other words, using the area model in algebra is just as easy as using it in fourth grade math. (And sometimes easier.)
Multiplying polynomials with the area model
Let’s say I wanted to multiply $5x^3+2x^2-7x+1$ by $x-4$. Most textbooks will show this with a line-by-line double-distributing (my word, not an official math term) method:
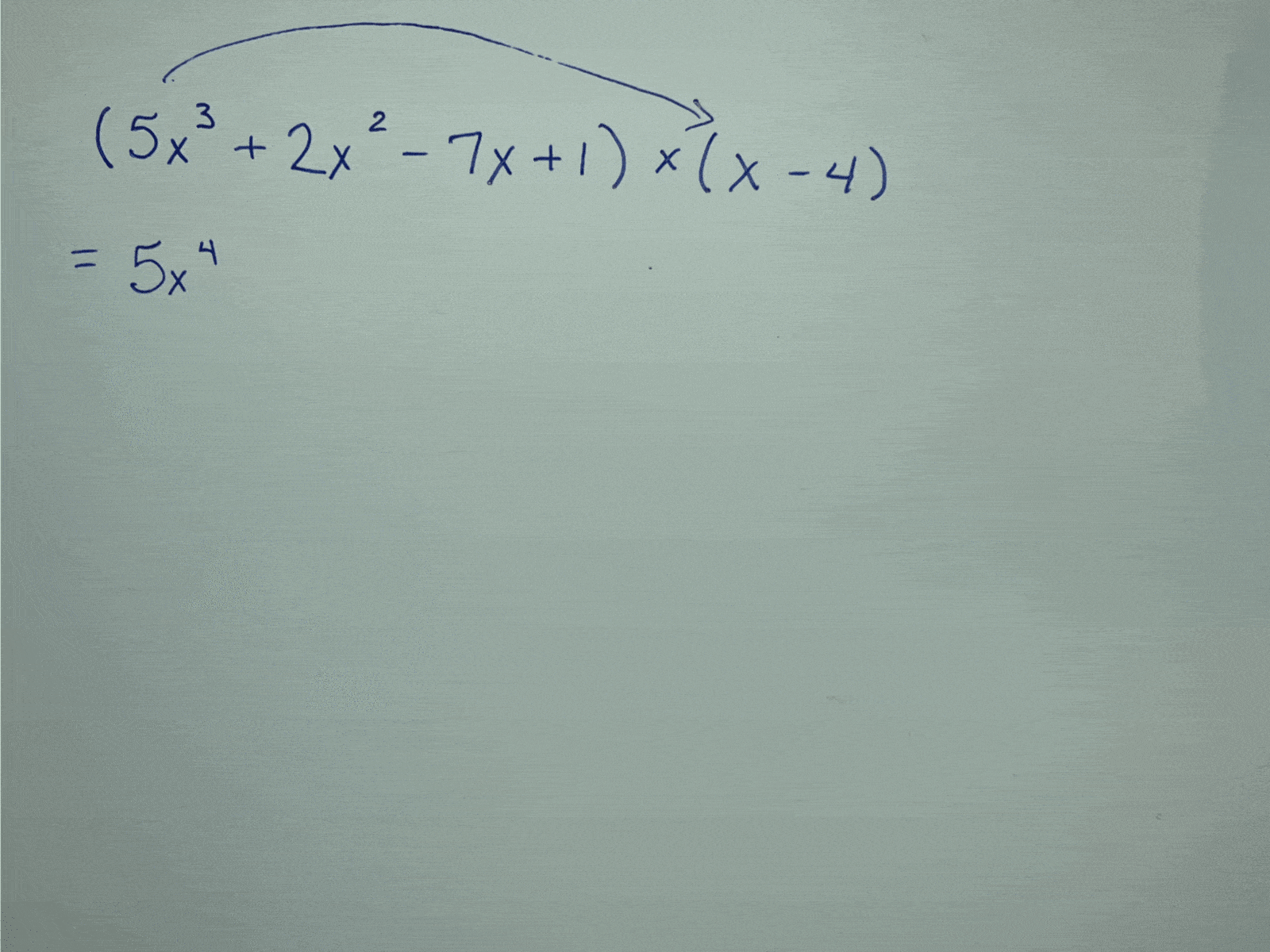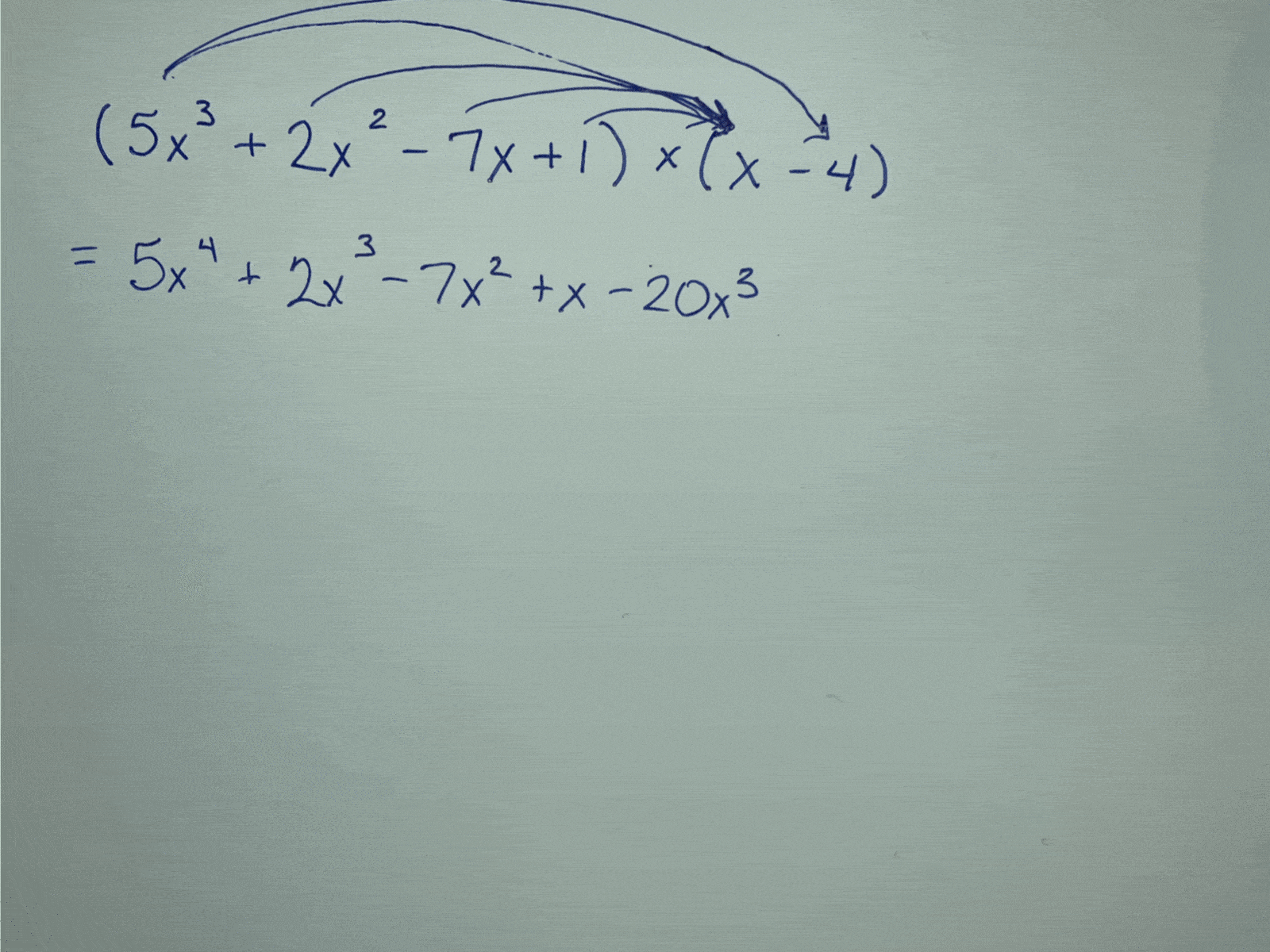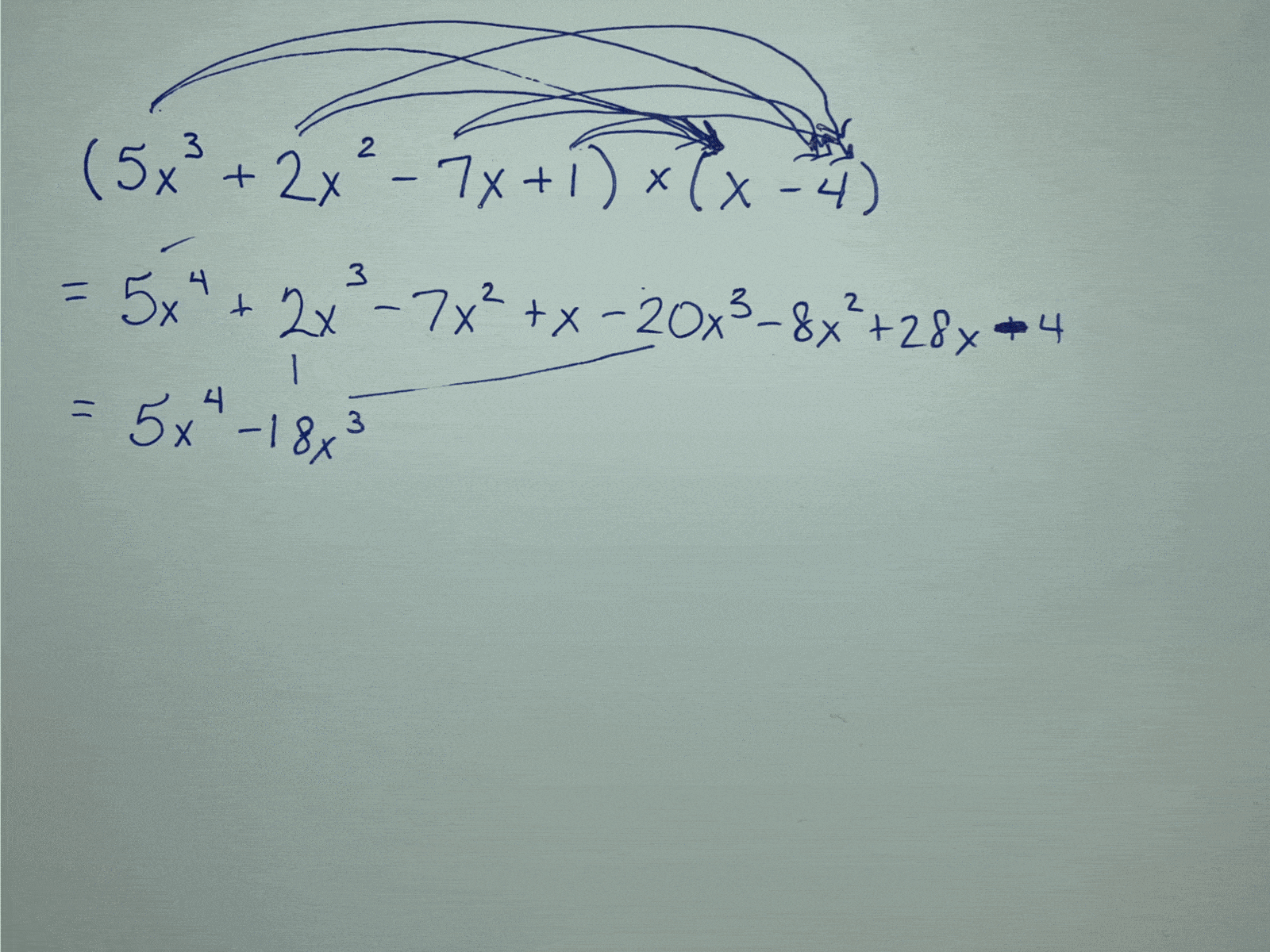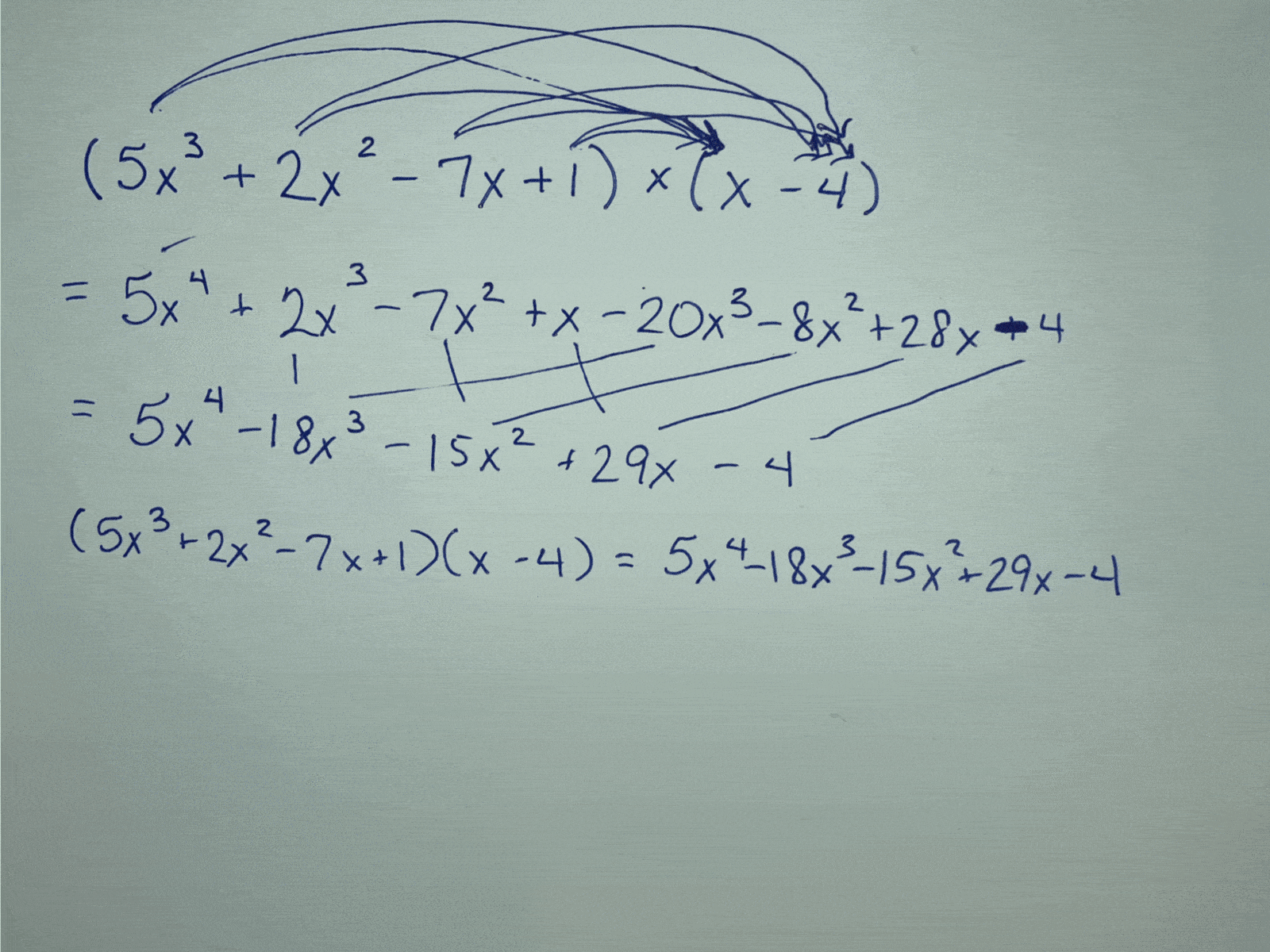
However, if we treat each term of the polynomial as though it’s a place value in an expanded form, an area model becomes easy to set up and works as a great organizational tool for multiplying this out:
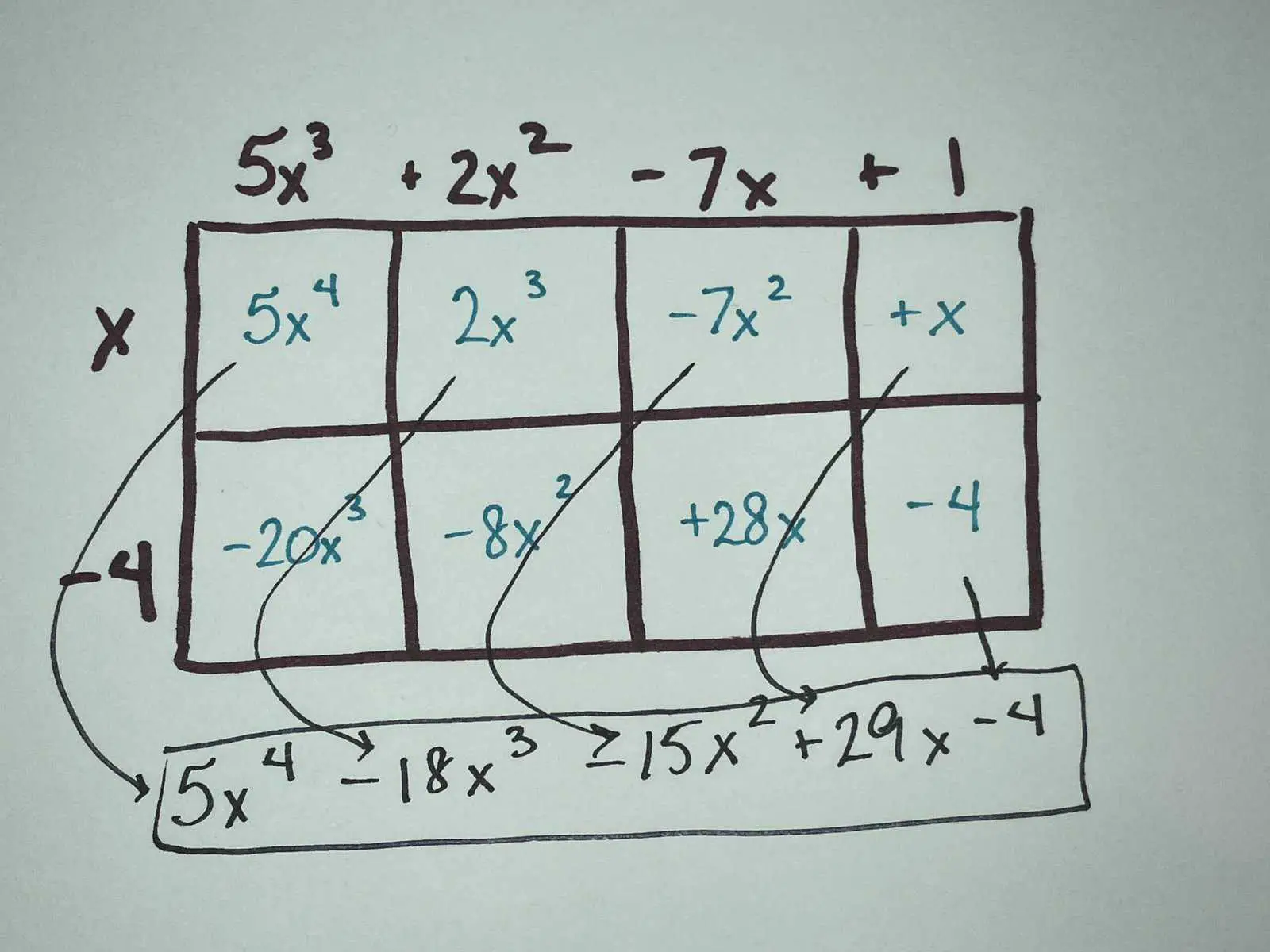
Of course, this comes with some of the same strengths and weaknesses of multiplying with the area model in general. However, in my personal opinion, it stays useful for larger polynomials than it does place values.
Factoring polynomials with the area model
One way to think of factoring, and the way it’s often taught, is that factoring is unmultiplying. Whether you’re factoring a number of a polynomial, you’re looking for what can be multiplied together to make this product. Thus, factoring is a lot like division. Just like we can use the area model for division, we can use it for factoring polynomials. However, I personally find the area model to be more useful in factoring in algebra than it is in dividing numbers. In part this is because the individual terms pose some limits on the factors we can choose/find. In part this is because we deal with, make use of, and don’t shy away from negative numbers.
In essence, we compare term-by-term the leading term of the divisor to each term in sequence of the quotient, ask how many times it divides into each subsequent term, multiply out by the full divisor, subtract away, and repeat.
Algebra Tiles – movable, physical algebra based on the area model
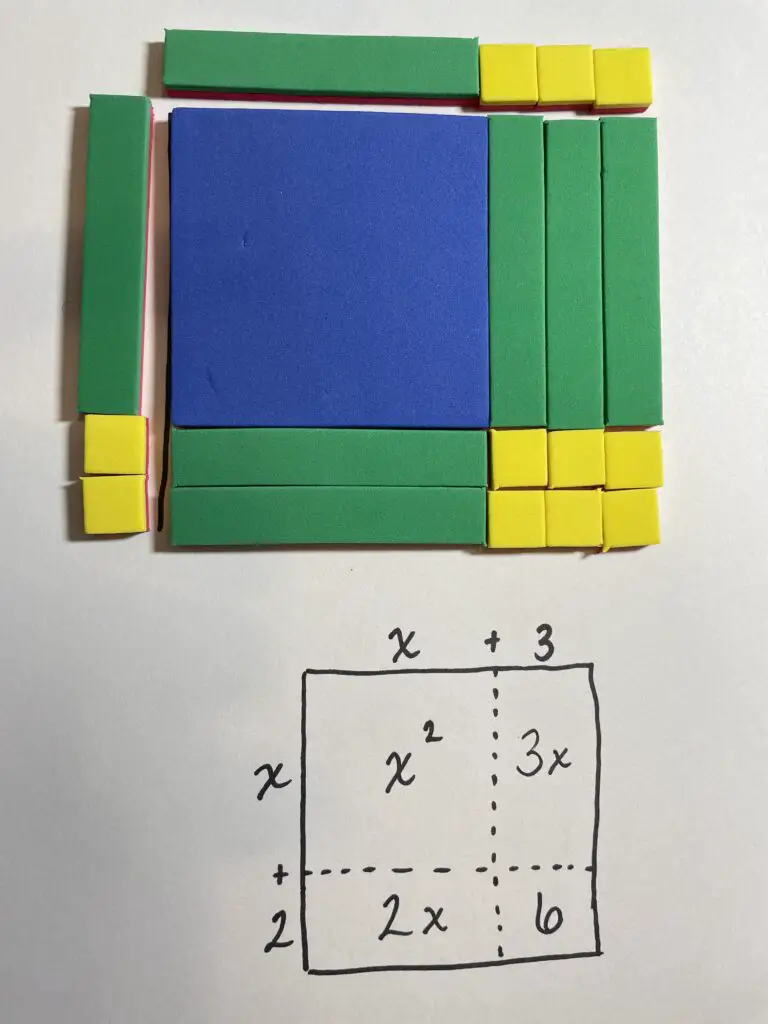
Algebra tiles are a common manipulative in the early stages of learning many algebra concepts. Algebra tiles are small tiles that can be moved around to represent the boxes you might see in a drawn area model. Learners can literally move the tiles and explore different ways of making area model rectangles without having to draw, redraw, erase, etc. It becomes a kinesthetic experience of learning.
Algebra tiles have their limitations, however, so are usually best used in the early phases. Their primary limitation is that they only represent polynomials up to degree 2 (squared). (This would be like limiting the area model to 2-digit numbers.) Algebra tiles also get a bit complicated to explain and understand once negative numbers get involved (still totally doable, just less obvious).
I discuss algebra tiles in several posts throughout this blog. To learn more about how they can be used, check out the algebratiles tag.
In summary, the area model is one of the most versatile models and tools in math. Its basic premise can be used across mathematical topics and grow with the learner throughout their math career. It lends visual organization and interpretation to various multiplication and division (or factoring) problems and lends to deeper connections between arithmetic, geometry, and the intriguing study of dimensions. With the basics here and in related articles, play and explore. See what you can learn and what connections the area model can build and strengthen in your own mathematical brain. Until next time…
You’ve Got This!
