The area model’s true strength is in multiplication. However, division bears a close enough relationship (they are inverse operations) to multiplication that we can use the area model to divide as well. In fact, the relationship is so close that we can think of division as “multiplying by the reciprocal.” Once students learn this view in prealgebra, some algebra teachers even claim “division no longer exists. It’s all multiplying by the reciprocal.” However, here we’ll think of division in the mid-elementary-school way: of splitting up a total into equal parts. At the same time, we’ll use the multiplication tool of area model to do that splitting up.
If you want to know more about the area model, check out my post Area Model Math or the collection of related posts under the Area Model tag.
This post was originally published on mathteacherbarbie.com. If you are reading this somewhere else, you are reading a stolen copy.
How to set up area model division
Division is the inverse operation of multiplication. In other words, we can think of it as multiplication’s opposite or a way of undoing multiplication or unmultiplying. It flips multiplication around, giving us the product (or the result of the related multiplication fact, known as the dividend in division) and one of the factors of the related multiplication fact (known as the divisor in division). A division problem asks us to find the other factor of the related multiplication problem (known as the quotient in division.).
In other words, our setup for a division area model problem has us looking for one of the sides of the rectangle, not the area.
If we wanted to compute $30618 \div 42$, we would set up our rectangle with $30618$ inside representing the total area and $42$ along the left-hand side representing the height. Then we would will look for the width of the rectangle to answer the problem.

Image created in Polypad by Mathigon.org
How to perform area model division
Before we get very far in this problem, we need to think about multiples of 42. We can get by with just a few multiples if we want, or we can write out as many as we want. The more multiples we write out now, usually the less work we have to do later, but not always. It’s a balancing act. I think I’ll stick with the “simpler” multiples that I might be able to do in my head ($42 \times 1$, $42 \times 2$ (doubling), $42 \times 3$ (double-double), multiplying by powers of 10 (sticking zeros on the end), and $42 \times 5$ (half ten)). Again, you can list different or more multiples if you want. There’s no hard or fast rule here. Fewer multiples will probably mean more steps in the problem, more multiples will (probably) mean fewer steps later.
| How to compute easily | shift place value (put zero at end) | another zero | yet another zero | |
| $42 \times 1=42$ | $42 \times 10 = 420$ | $42 \times 100=4200$ | $42 \times 1000=42000$ | |
| double | $42 \times 2=84$ | $42 \times 20=840$ | $42 \times 200=8400$ | |
| double-double | $42 \times 4=168$ | $42 \times 40=1680$ | $42 \times 400=16800$ | |
| half-ten | $42 \times 5=210$ | $42 \times 50=2100$ | $42 \times 500=21000$ |
My next step differs just a little from others on the internet. In concept, it’s the same, the difference is in strategy of splitting up the 30,618 area. My way reduces visual clutter and, I believe, help us understand better what’s going on and make more connections. Most other presenters on the internet attempt to minimize the number of steps we take. Since these days we are more concerned with understanding and less concerned with speed, so I’ll go the comprehension route.
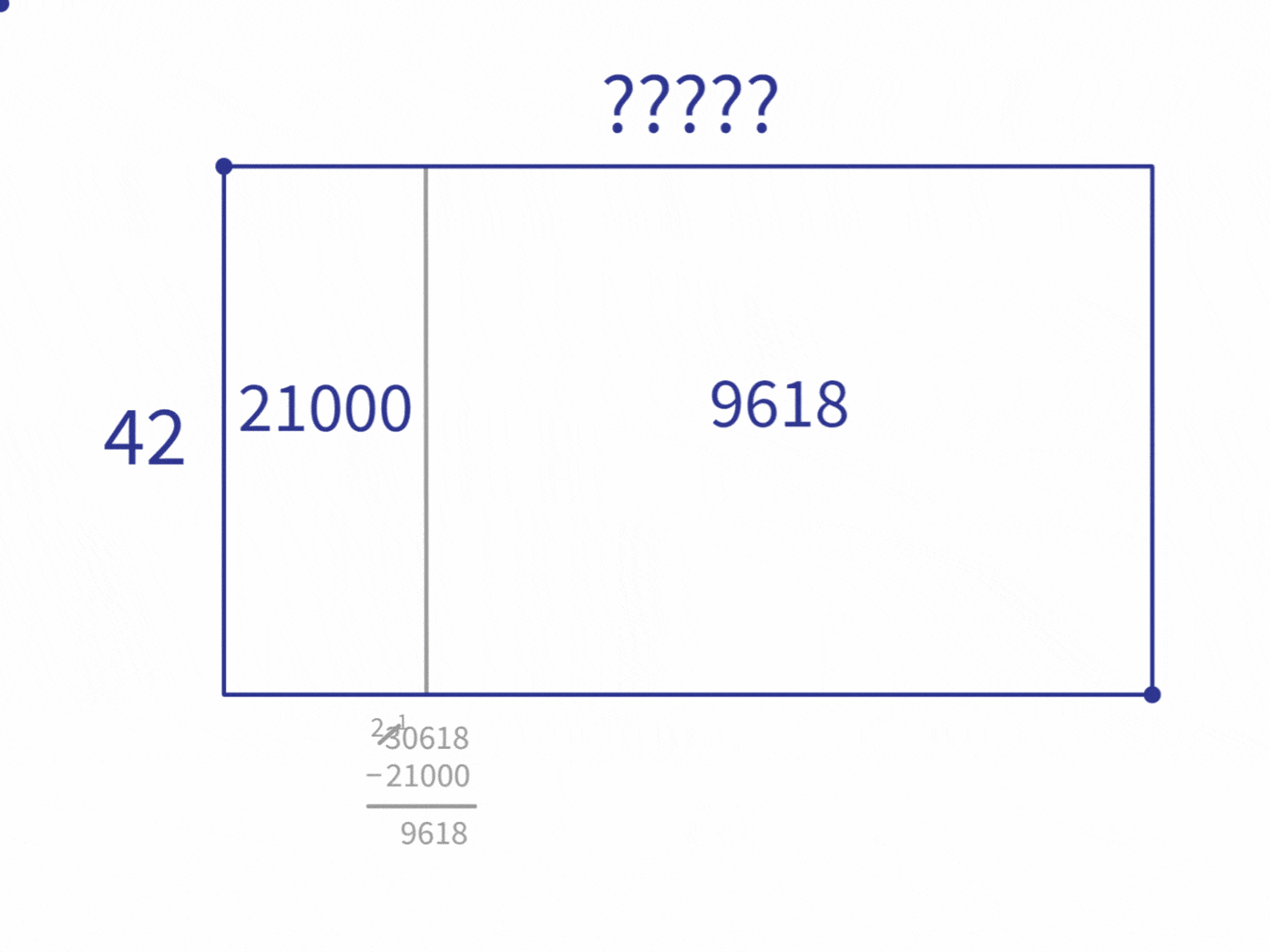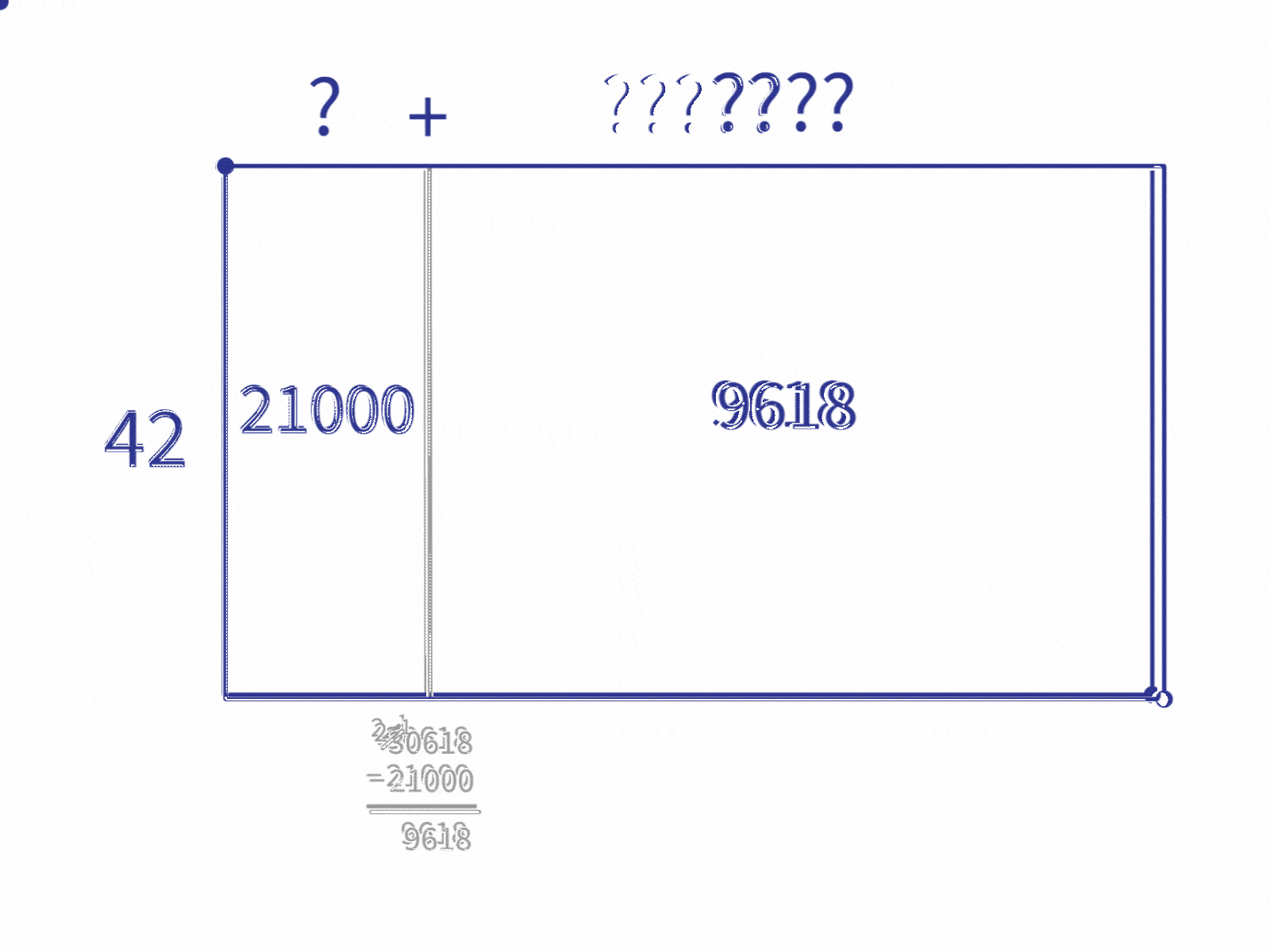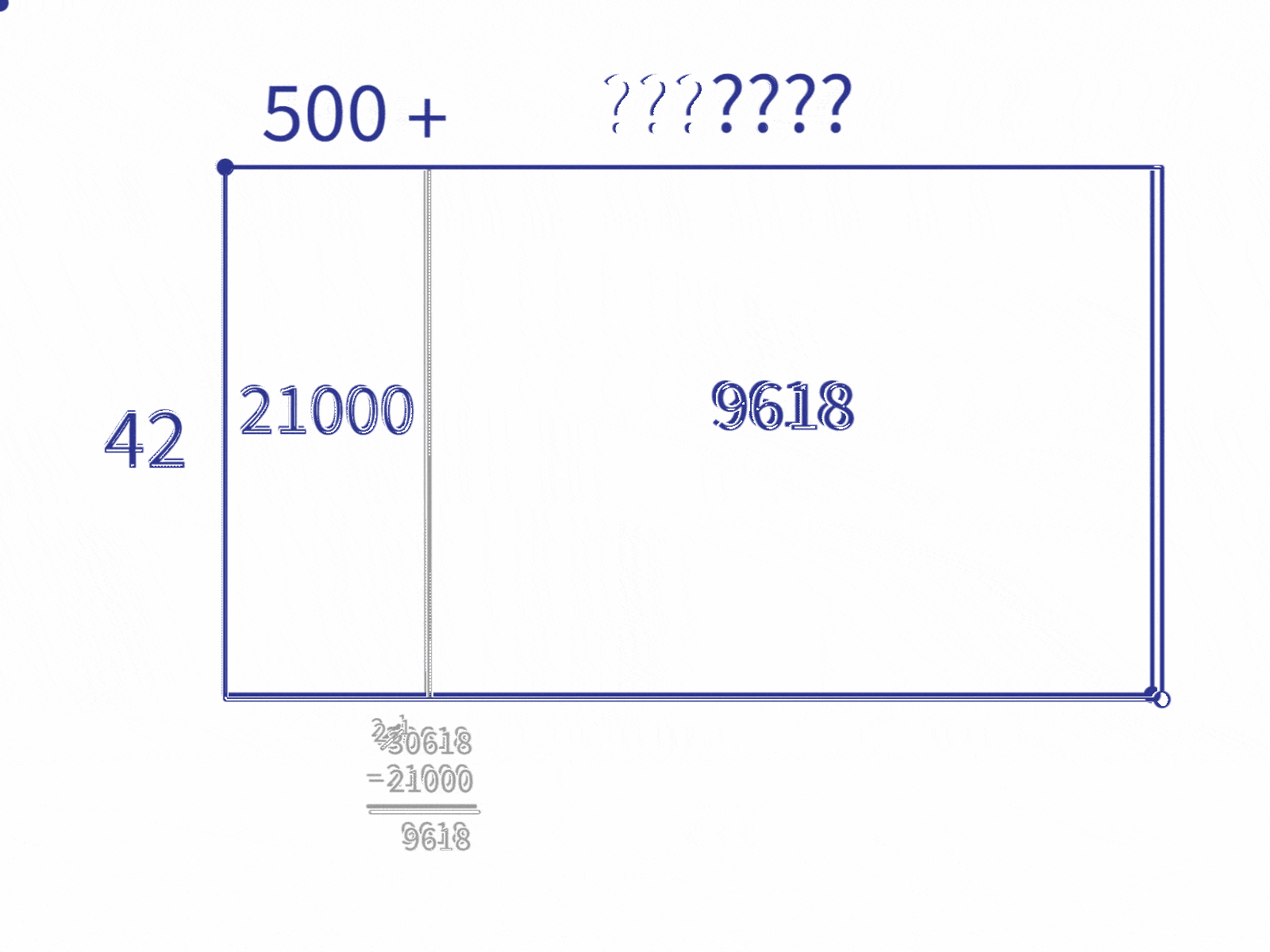
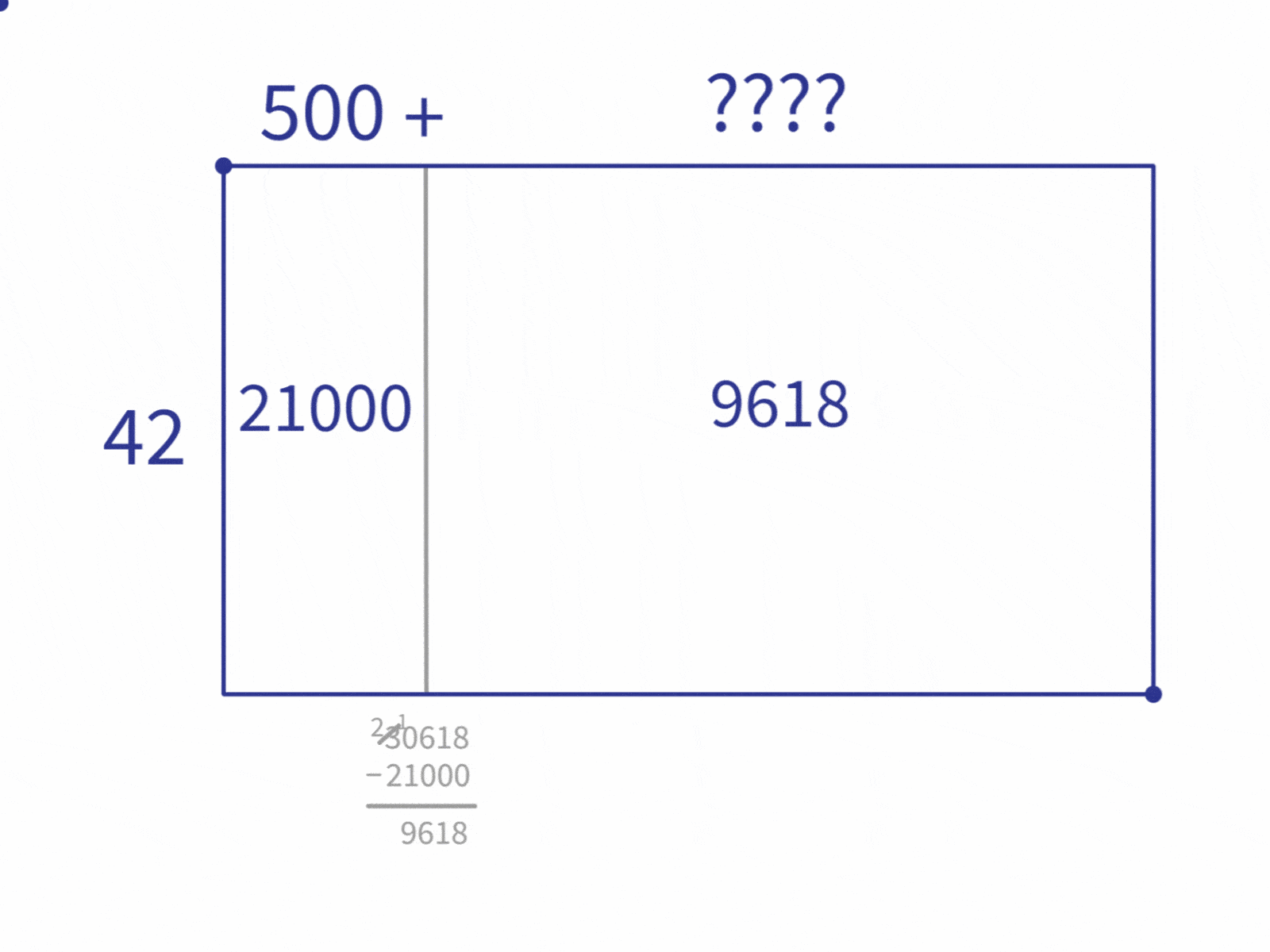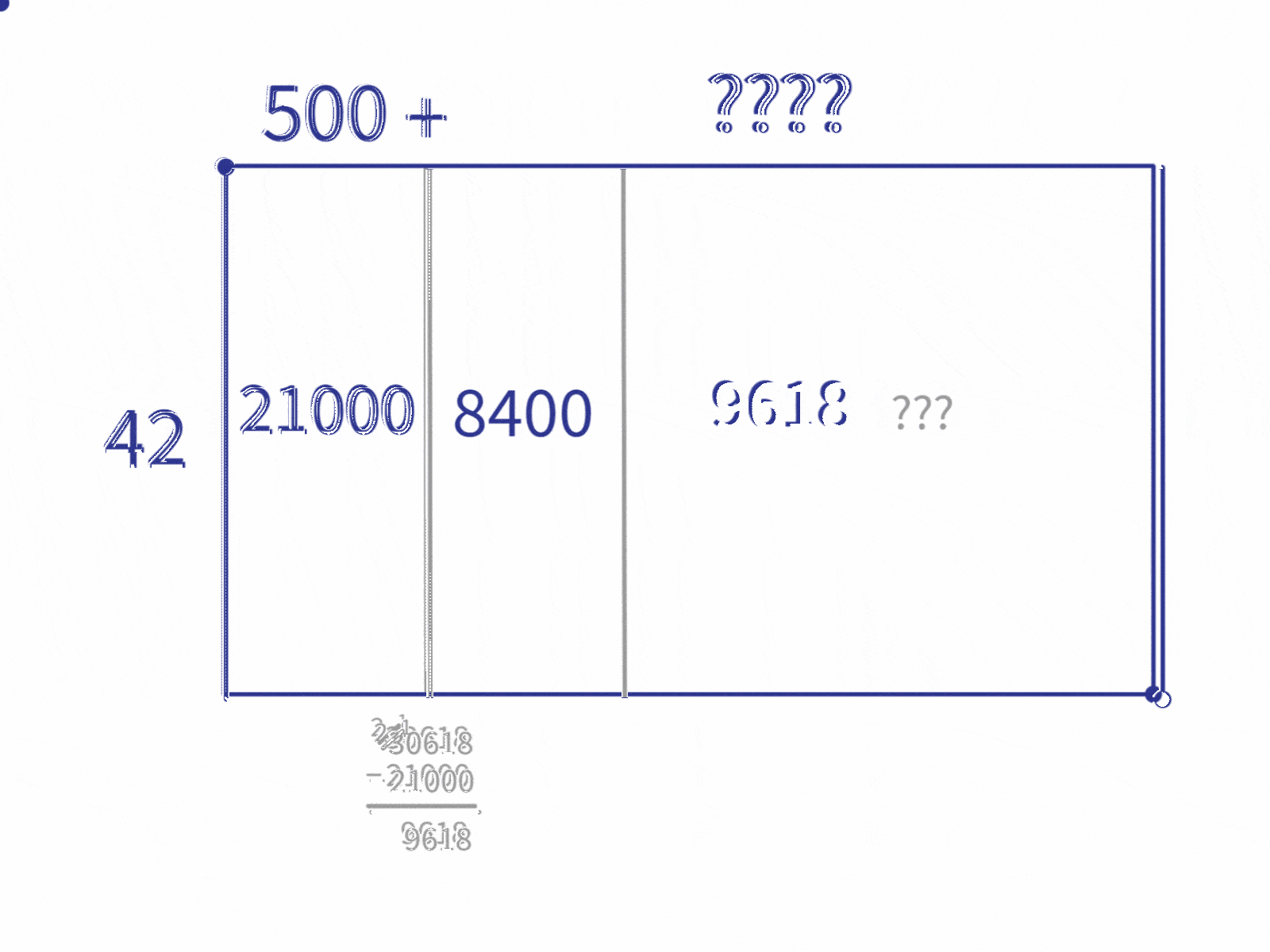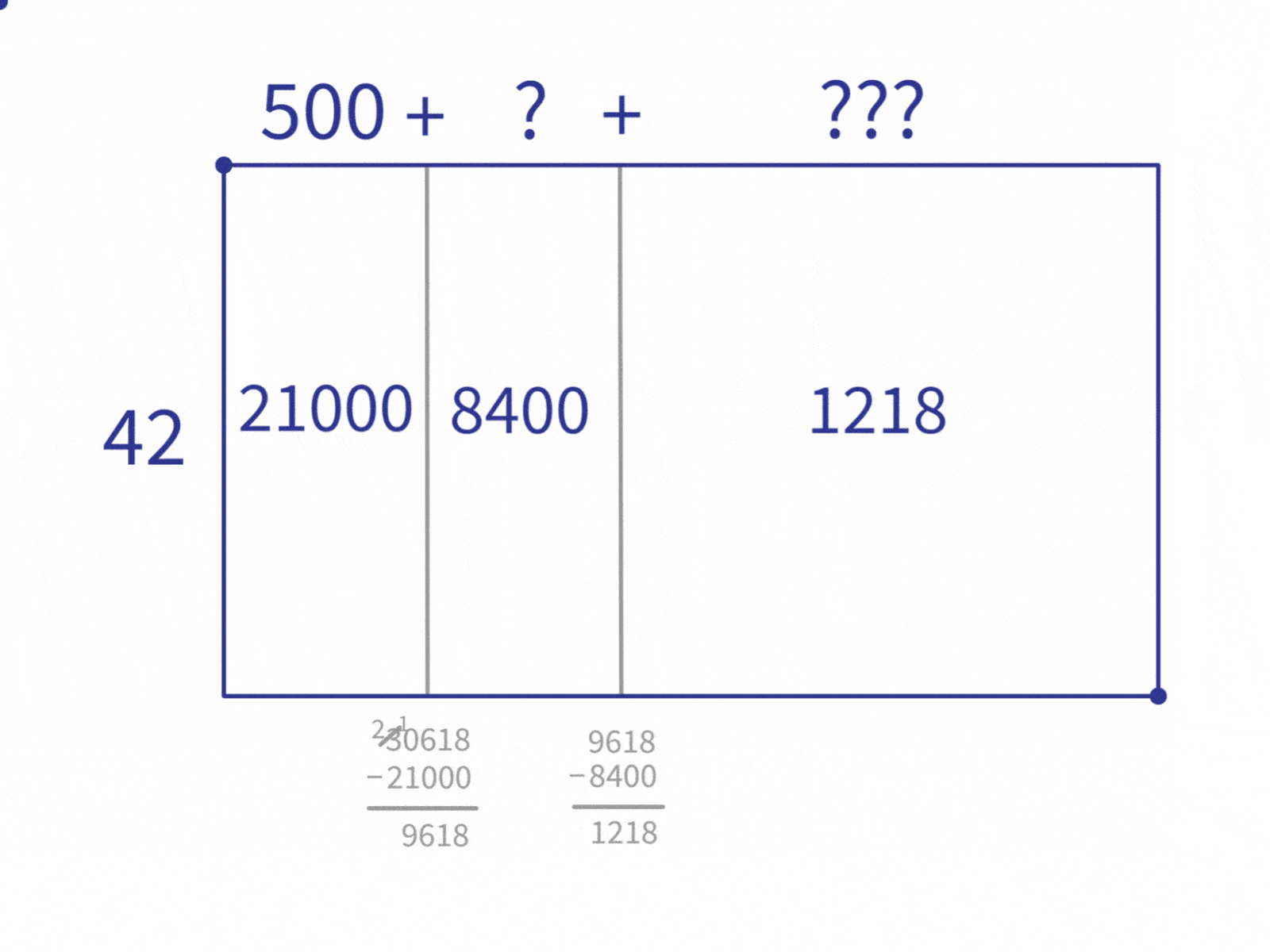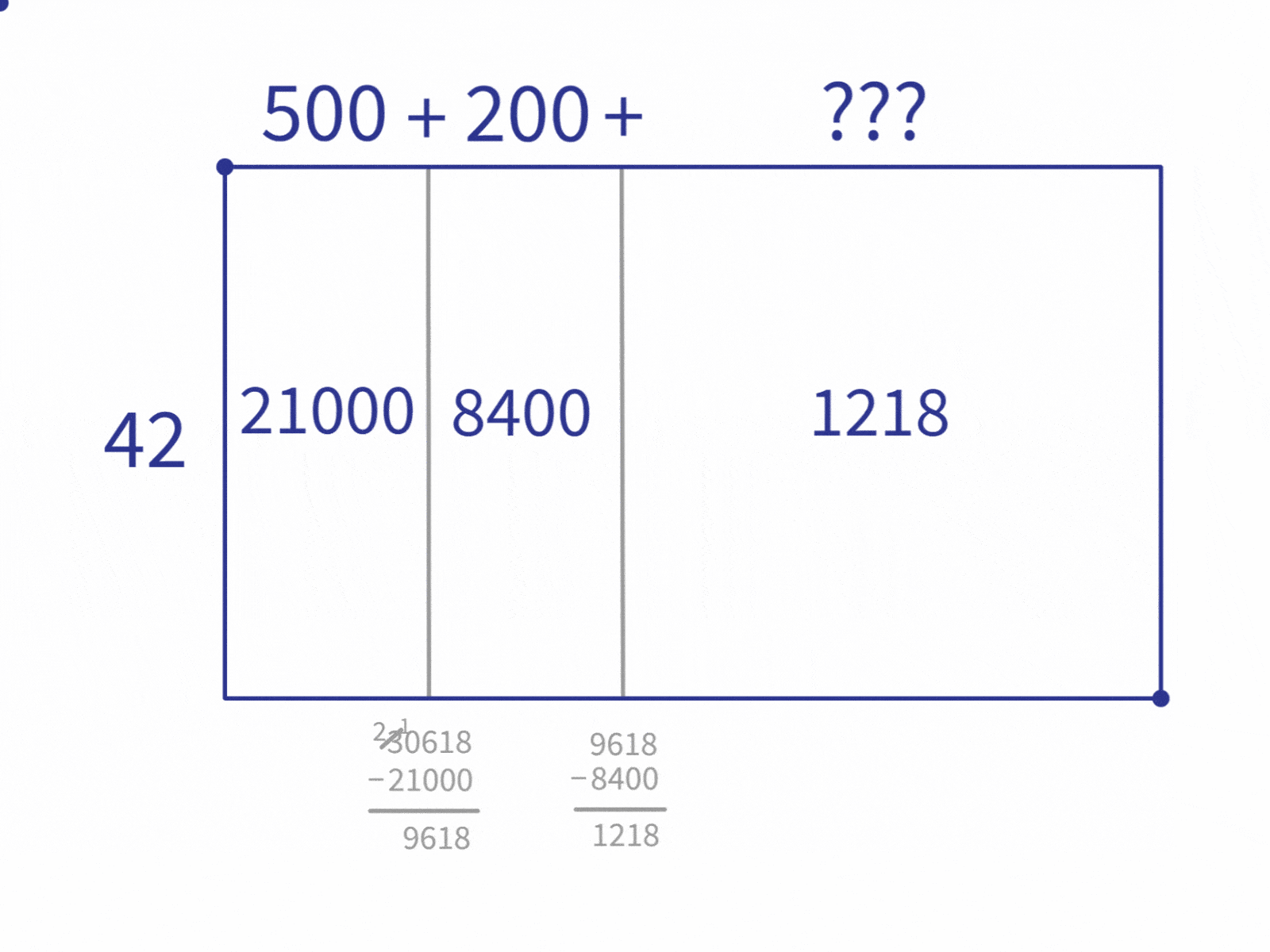
Let’s look at the table of multiples we created. What’s the biggest multiple in the table that’s still smaller than 30,618? That’s 21,000 ($42 \times 500$). So, let’s split the rectangle into one part that’s size 21,000 and another part that has the remaining 9,618 ($30618-21000=9618$).

Since we know from our prep work that $42 \times 500=21000$, we can write $500$ as the length of the $21000$ block.
Then we repeat the steps to break down the “remainder” block into the multiples we figured out earlier. If we look back at our table, we see that 8,400 ($42 \times 200$) is the biggest multiple from our table that’s still smaller than 9,618. So we repeat the process using 8,400.
We continue repeating this process. Each time looking for the largest multiple that is still less than the remaining area. (Note that this is the part of the process that can often be shortened by spending more time listing multiples at the beginning. As noted before, it’s a trade-off.)
The next step is to look for the largest multiple less than 1,218 ($840$, which is $42 \times 20$), split that area off, compute the remaining area. And repeat until we can’t fit any more of the multiples in.
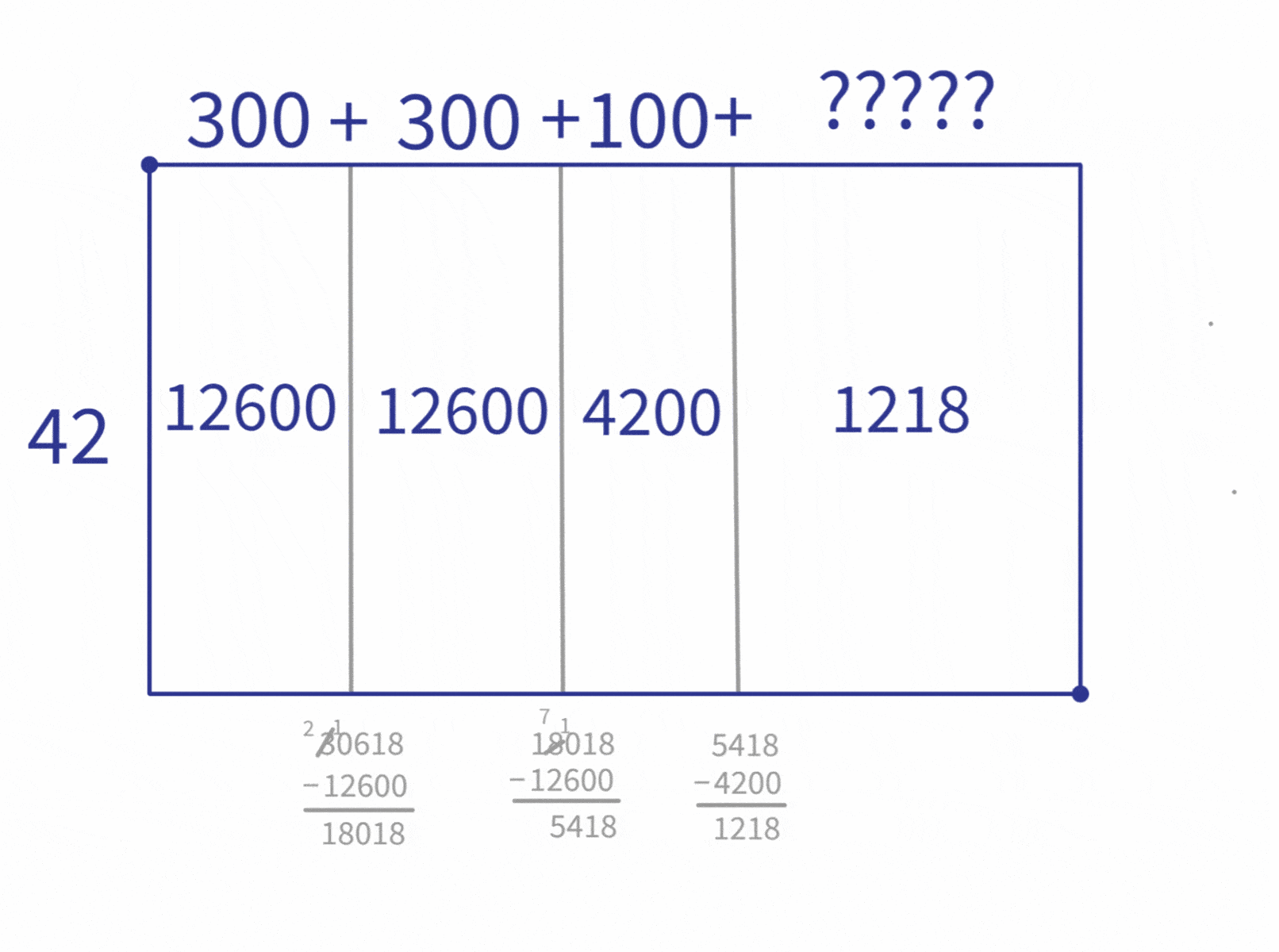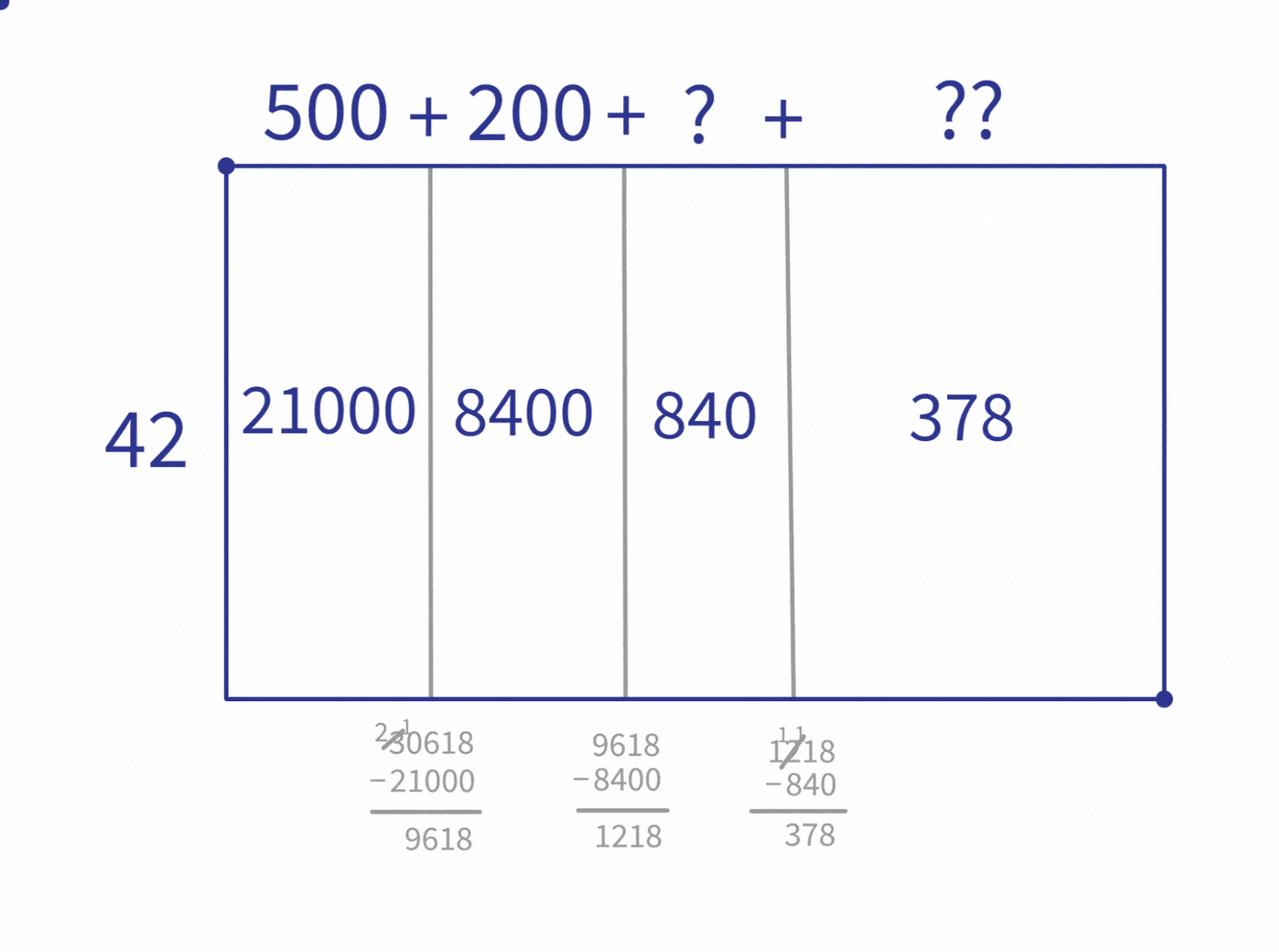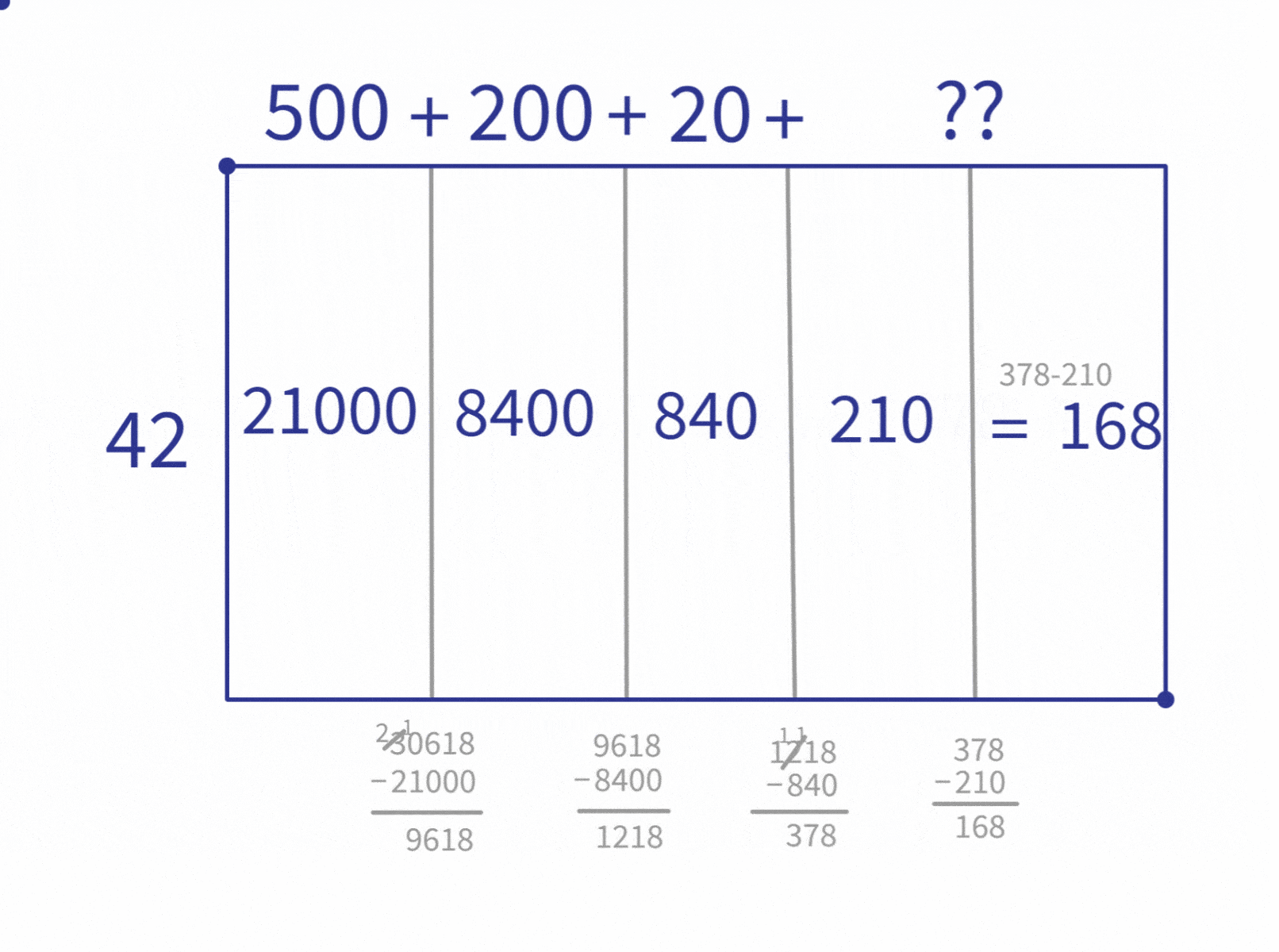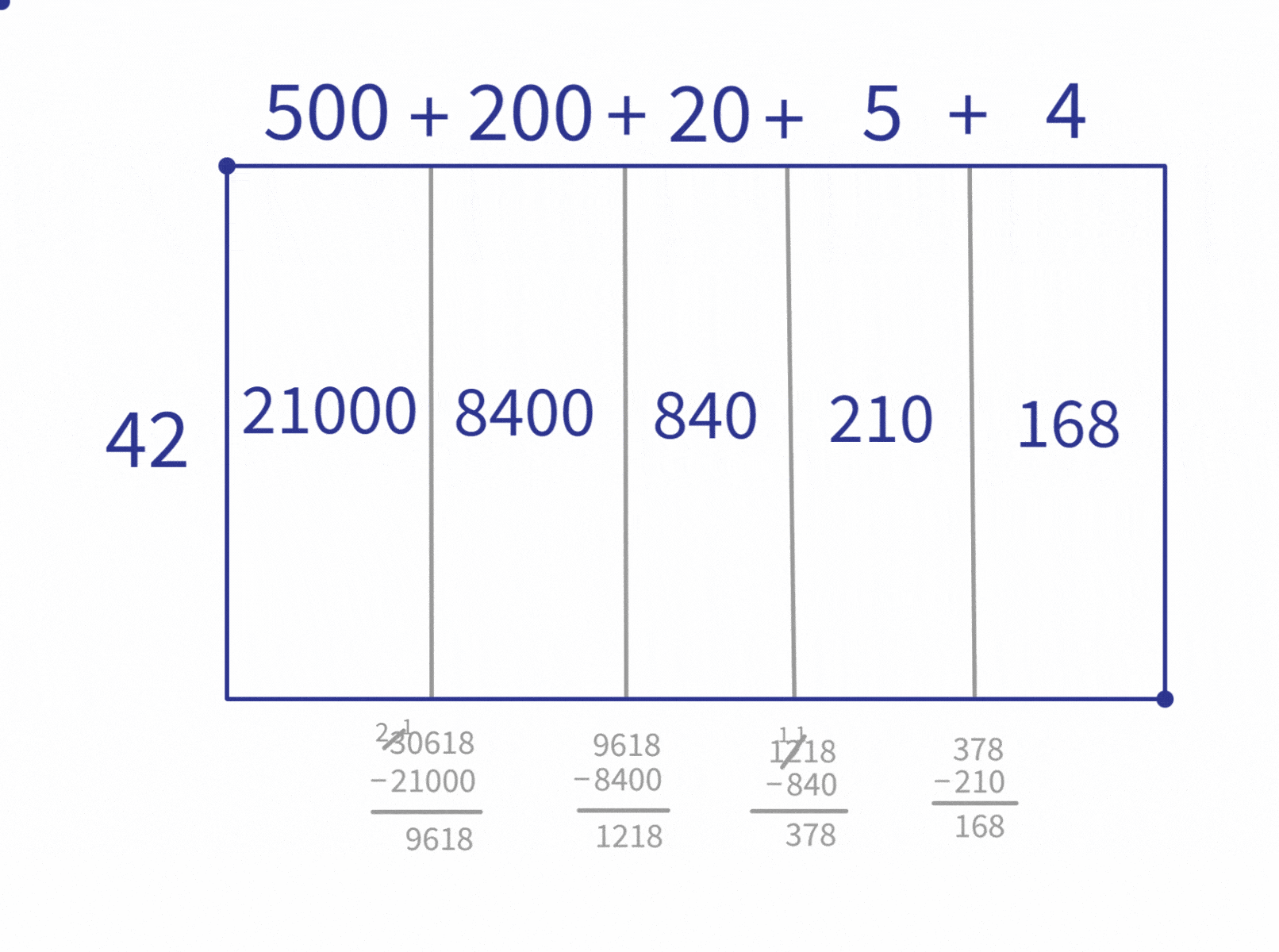
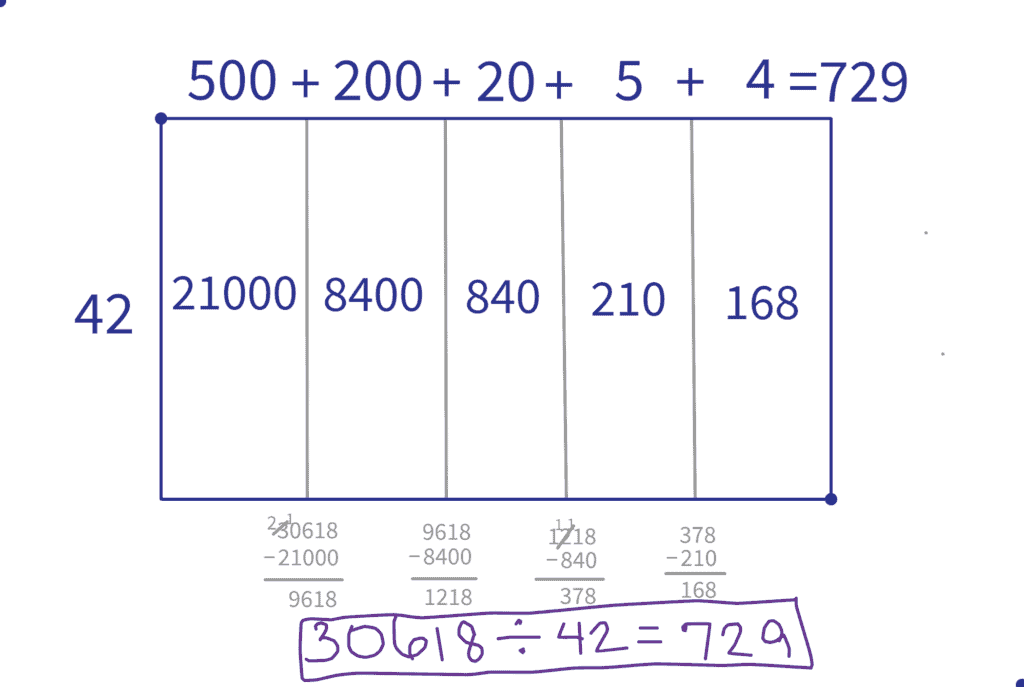
Finally, we add the lengths together and report out the final answer: $30618 \div 42=729$.
Remainders when it doesn’t divide evenly
Fortunately, the process of dividing with the area model is the same whether the numbers divide evenly or not. If we get to the end of the problem and we can’t find any multiple that’s greater than our divisor (the number being divided by), that’s when we know we have a remainder.
To illustrate, divide $30620 \div 42$, which looks a whole lot like the problem we just did ($30618 \div 42$) except right at the very end, where we end up with a remainder of 2. (If we had done that final subtraction in the example above, we would have found a “remainder” of 0, meaning that the problem divided evenly.)
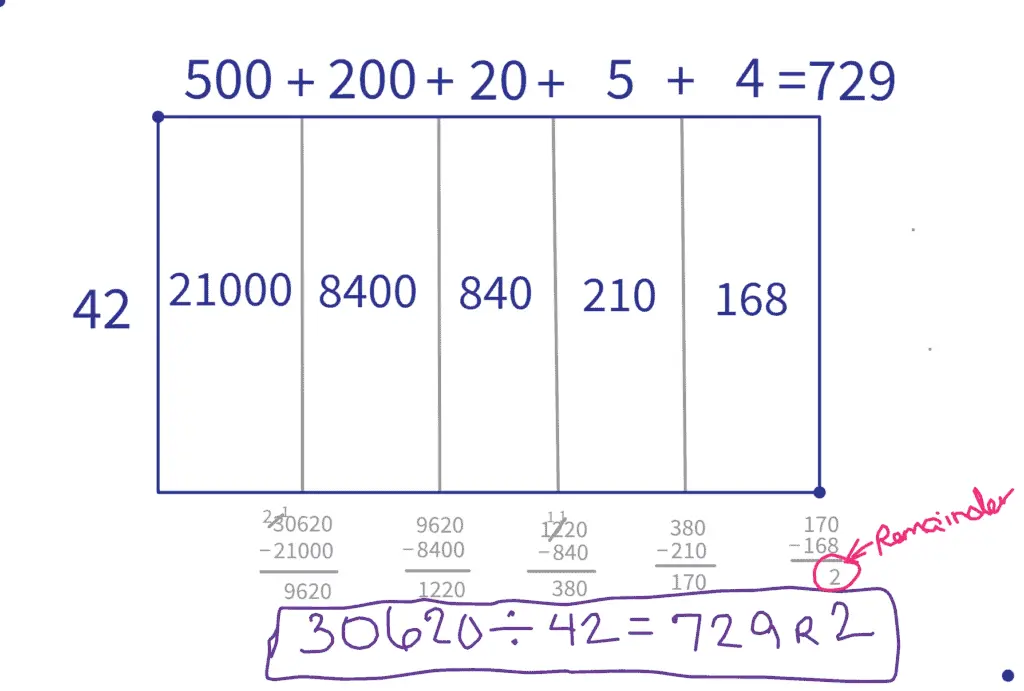
How does the area model compare to long division
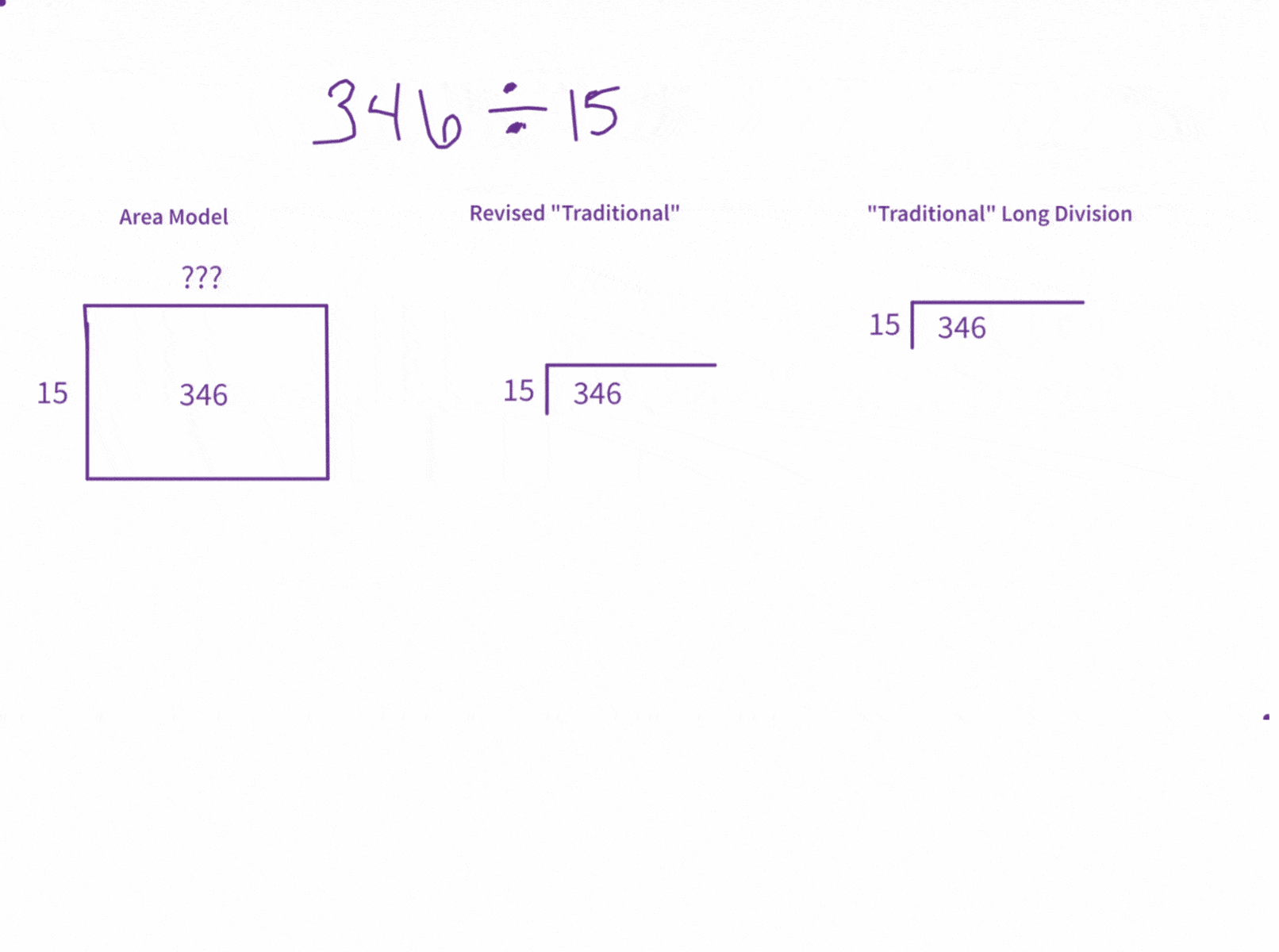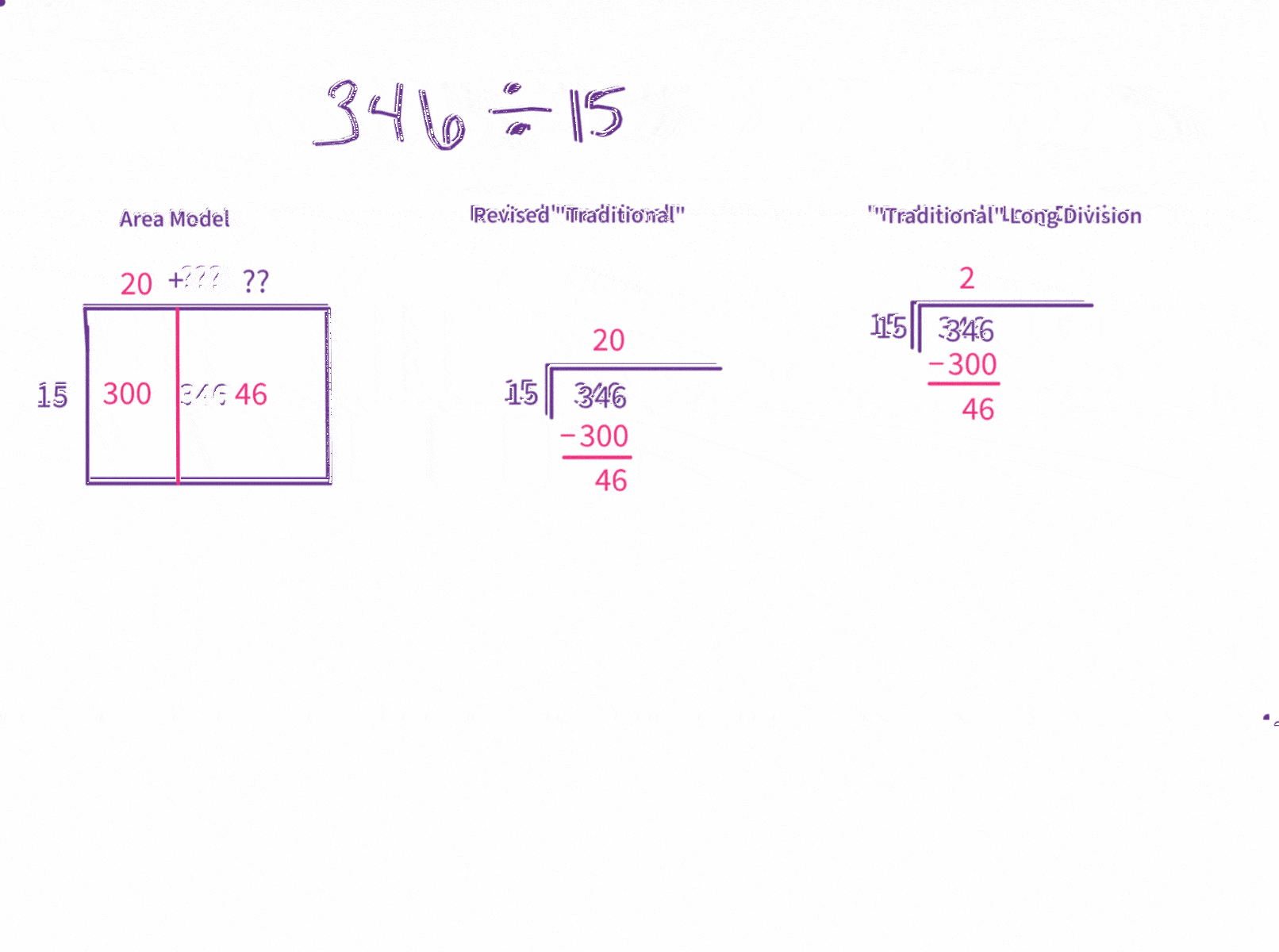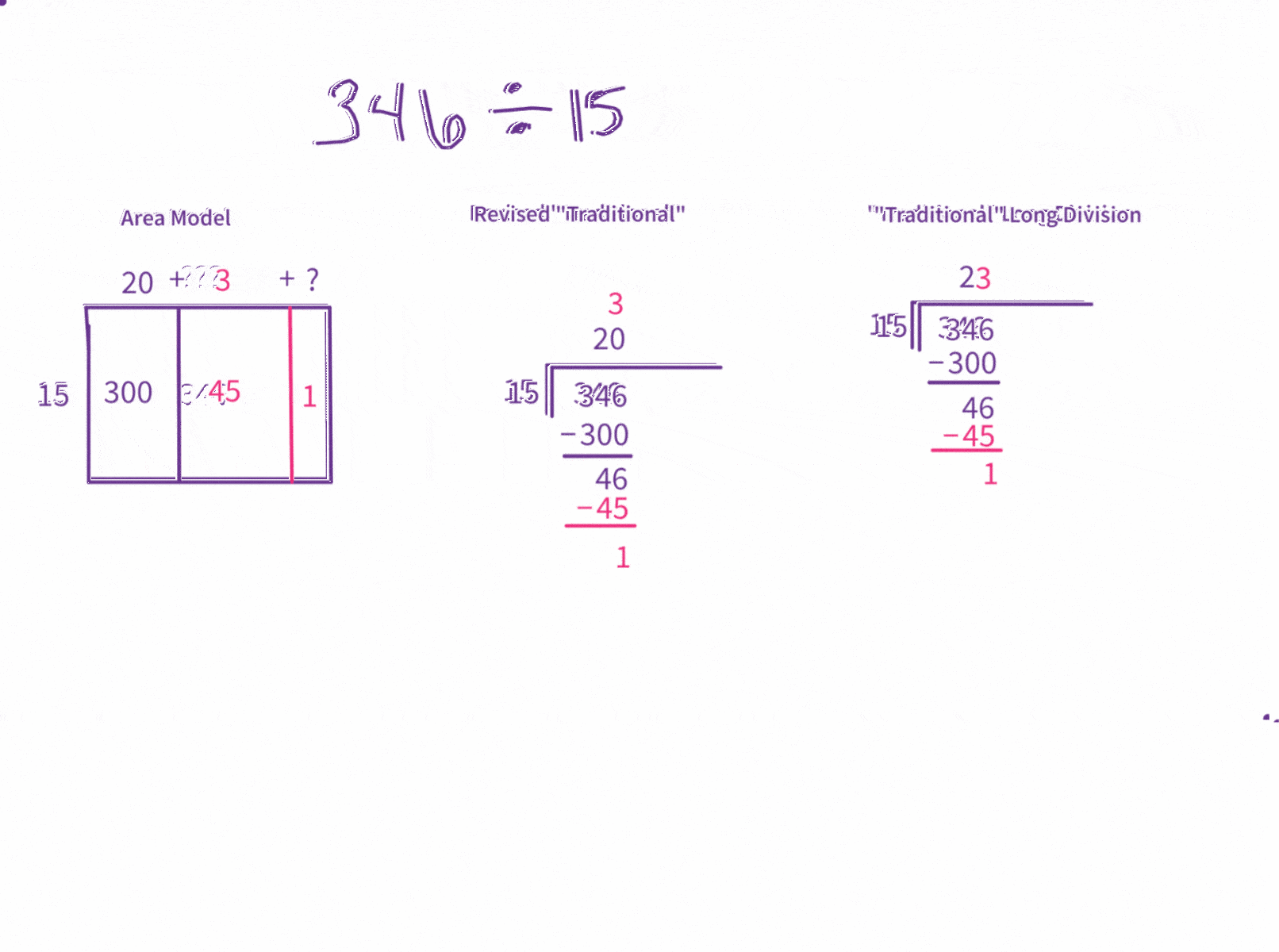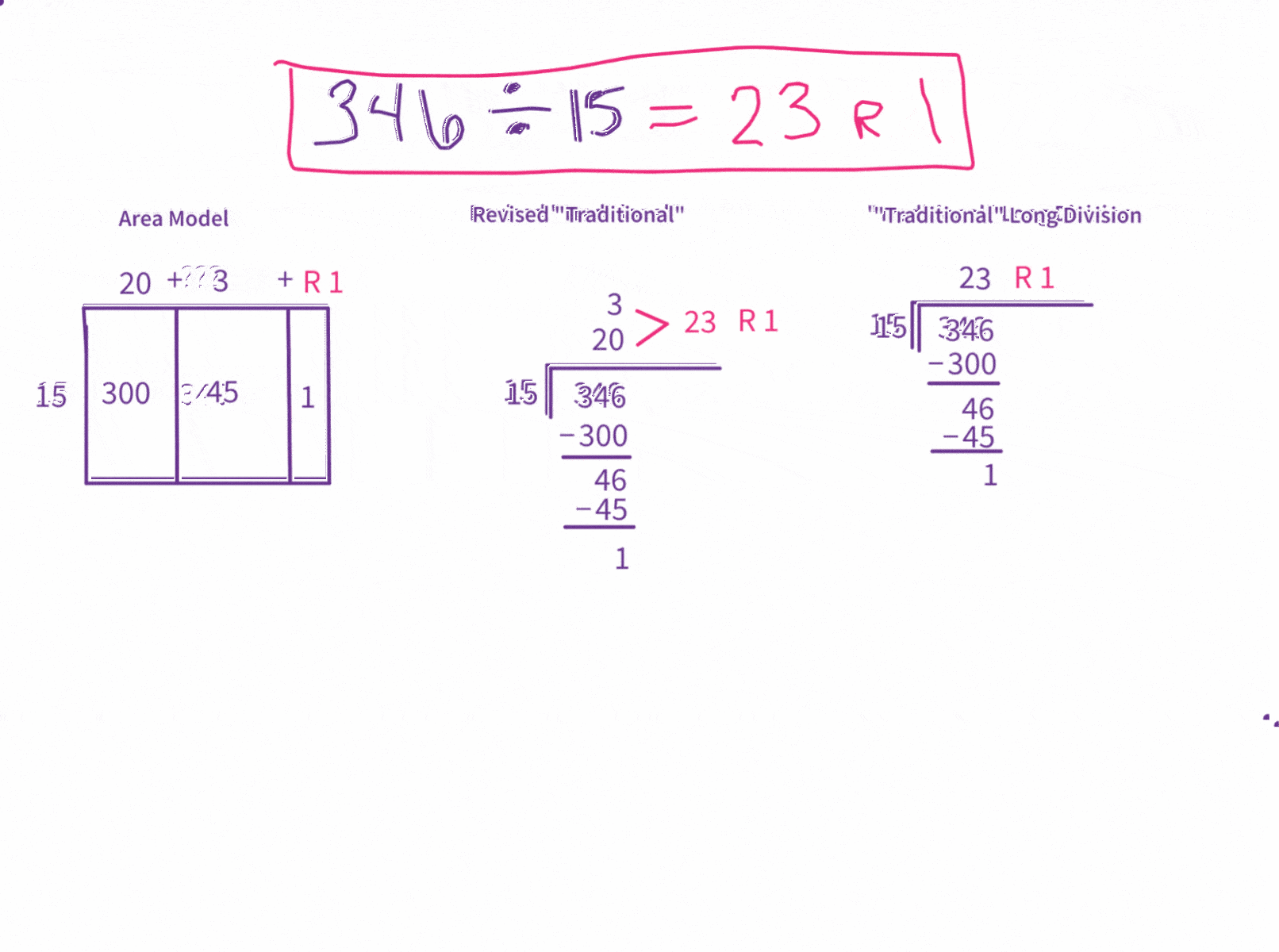
The outward appearance of the area model is obviously much different than the visuals of the long division algorithm. However, the procedure — the mechanics — of the division is very similar. The main difference is in how prescriptive the algorithm is regarding the starting-place of the division and which multiple is considered.
The area model is very flexible, allowing us to recognize various smaller area components as we see and notice them and allowing us to start with whatever multiple we see first. However, the “traditional” long division algorithm stipulates that we start with a certain multiple. If we force the area model to start with that same multiple, we can watch the two models side-by-side.
However, there’s also a third model, a different way of writing out the “traditional” algorithm that visually emphasizes place value while still using the same steps and reasonings as the short-form version. I will display that algorithm as a mediator to help bridge the area model to the more familiar — but less intuitive — “traditional,” “efficient” long-division algorithm.
You’ve Got This!
