Words we use loosely throughout elementary math — such as solve, expression, equation, formula — suddenly gain very particular and specific meanings in algebra. Not only do some algebra teachers become sticklers for vocabulary, but paying careful attention to the language can actually help you understand what’s being asked and what your next steps should be. The words formula, expression, relation, and function are closely related with subtle differences, and are often confused in algebra.
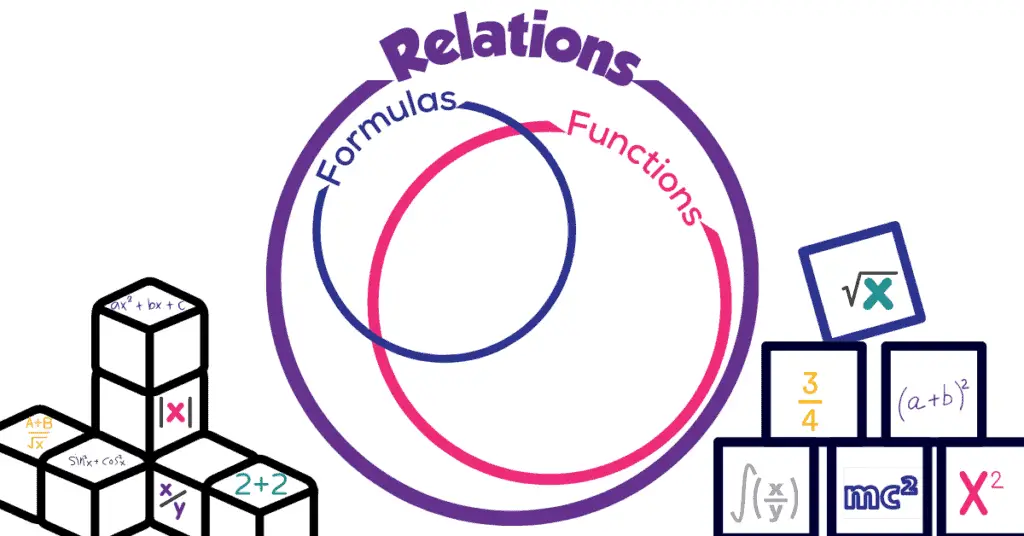
Formulas, relations, and functions in algebra are all made up out of combinations of one or more expressions. Formulas and functions in algebra are both types of relations, but some relations are neither formula nor function. Some functions are formulas and some formulas are functions, but not all.
This post was originally published on mathteacherbarbie.com. If you are viewing it elsewhere, you are viewing a stolen version.
Algebraic Expressions are combinations of numbers, variables, and operators (add, subtract, multiply, divide, exponents, roots, factorials, etc)
Only numbers, variables, and operators can be part of algebraic expressions. Expressions alone do not include equal or other comparison signs. Expressions in algebra are like phrases or sentence fragments in language. Equal signs and inequality or comparison signs are like the verb in a sentence connecting the subject and object. You can hear this happening quite literally when you read aloud a mathematical sentence such as 3+5=8. Compare the closure of that full sentence to the phrase “3+5” recited out loud. “3+5” is an expression. “3+5=8” is called an equation.
Algebraic Relations Show How Two or More Different Sets are Connected (or Related)
Relations define relationships, or connections, between two different sets (or groups) of elements. A collection of ordered pairs is a relation because is shows relationships between one set of numbers to a similar set of numbers — or how numbers from the input set are assigned to, transformed into, or paired with the numbers from the output set. Equations or comparison statements are also relations because they demonstrate how to expressions (one on each sign of the equal or comparison sign) are related.
Functions, in any form they are expressed, are a specific type of relation. Not all relations are functions, but all functions are indeed relations. The same can be said for formulas. Every formula shows a relationship between the variables involved in whatever system it describes. Thus, every formula is an algebraic relation (but not vice versa).
Formulas are relations between two or more variables that hold true even when one or both variables change
Formulas are almost always written or shown as an equation, or occasionally as an inequality. The variables almost always represent some quantity that has a specific and concrete interpretation (not just the generic inputs or outputs for example). Some formulas you may be familiar with are $d=rt$ (distance equals rate times time) or the area of a circle $A=\pi r^2$. In the first formula, each variable represents a different idea related to movement in a straight line. As often happens, the letters used relate directly to the words used for each idea.
We can also solve the $d=rt$ formula for a different variable to see in symbols that we would divide the distance traveled by the time it took to travel in order to learn how fast we went: $r=\frac{d}{t}$. The second formula, the area of a circle, also uses the variable $r$. However, in this case $r$ has a different meaning. In our first formula, $r$ stood for rate, but for the circle, $r$ stands for radius. Any time we are working with formulas, it is useful to know the context.
It’s also useful to know the units each item is measured in. In our revised $r=\frac{d}{t}$, is our final rate in miles per hour, meters per second, feet per minute? We can’t know this unless we also know the units our distance and time are measured in. In formulas, the relationship holds true regardless of the specific units our variables are measured in. However, changing the units would also change the numbers as well as the units we would assign to the missing information. This is part of the power of formulas.
Functions describe a reliable, predictable assignment of one set to another
Functions are a special type of relation. A relation that is both reliable (every time I put an individual input into the relation, I get out the same output) and predictable (a set of rules that leads everyone to get the same output any time they start with the same input). These two characteristics of functions lead to the common definition that a function is a relation that assigns one input to at most one output. If it assigned an input to more than one output, then the assignment wouldn’t be either reliable or predictable because you could get different outputs out. Sometimes functions can’t assign certain inputs to any outputs. This can still be a function — we would just say that input isn’t in the domain of the function. More about domains is a topic for another post.
Let me know if you still have questions about the differences. And in the meantime, remember…
You’ve Got This!
