We can add numbers — even large numbers — without carrying. Carrying is really just a shorthand notation for thinking of 10 units in one place value as 1 unit in the next place value. Thus, it’s one version of regrouping: making 10 ones into a single group of 10, making 10 tens into a single group of 100, etc. If we think of other regrouping strategies, we can actually play with the numbers in a variety of ways to make new, easier problems that still give us the final sum we need.
This article was originally published on mathteacherbarbie.com. If you are reading it elsewhere, you are reading a stolen version.
Easiest addition problems
Addition is easiest when there are lots of zeros.
The number $0$, or zero, is what we call the additive identity. In other words, when we add $0$ (“additive”), we get the number we started with: the number we added to keeps its “identity” after zero is added. Any number plus $0$ is that number itself.
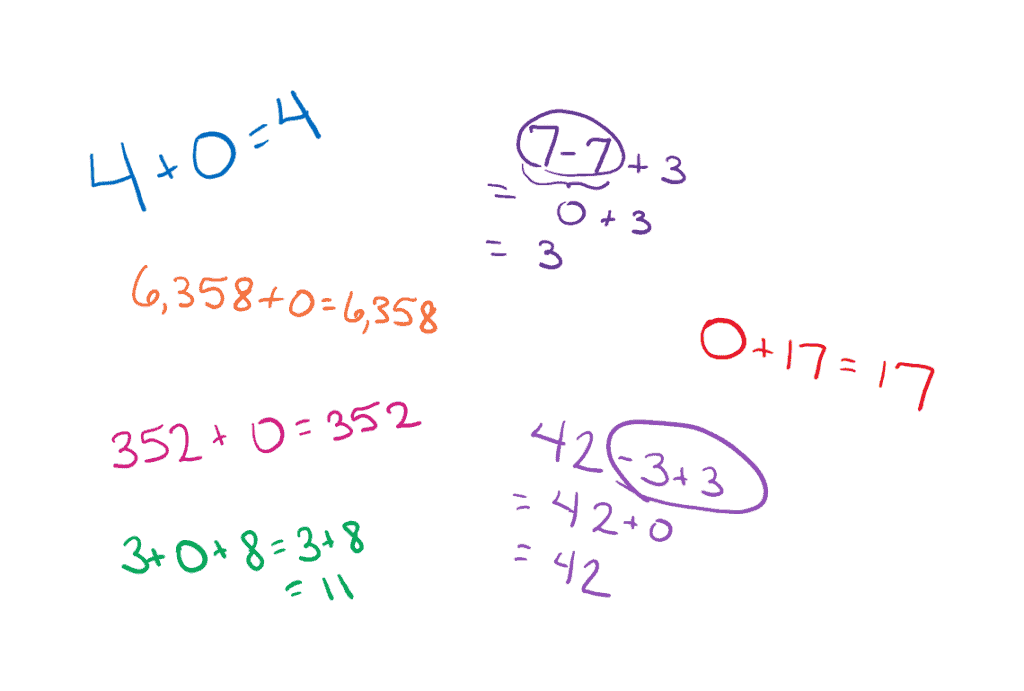
This property of zero makes adding $0$ trivial. Helpfully, it also makes adding easier when there are zeros holding place values, such as when adding $10$ or $500$ or $4,006,000$. If we can maximize the number of zero place values in our addition problem, we can make the overall problem easier.
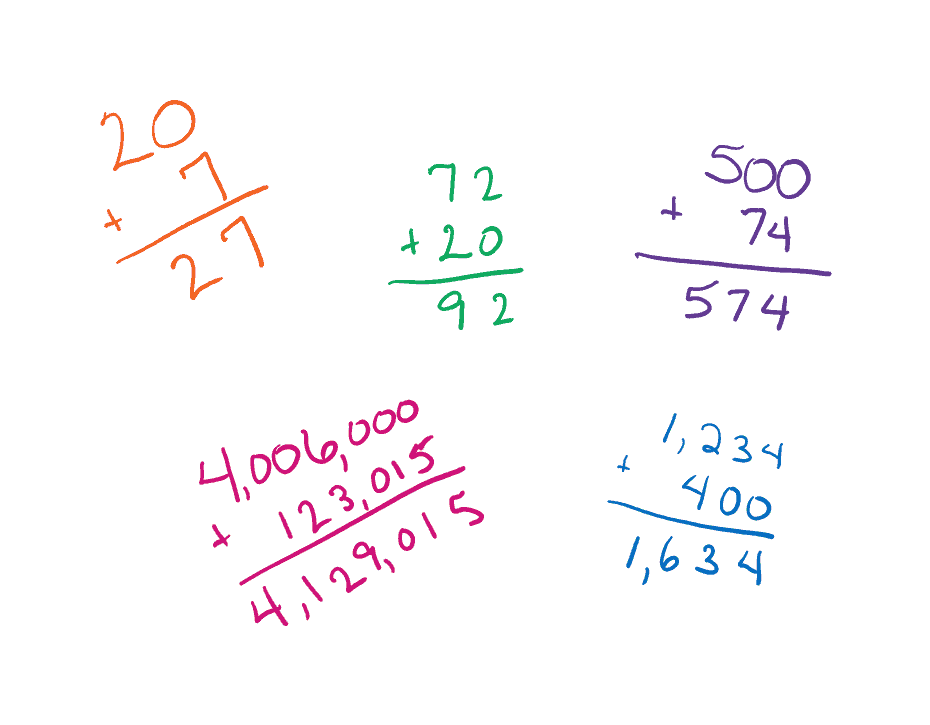
Making harder problems easy
Let’s start with a problem that’s not too very hard. Maybe something like $17+9$. You might be able to do this problem in your head without thinking too much. Great! Then you can check the final answer for the rest of us.
This problem doesn’t have any $0$s in any of the place values. Not only that, but the $7$ and the $9$ in the ones places are both “big” and close to $10$. Wait… they’re close to $10$. Maybe we can use that.
$9$, in fact, is really quite close to $10$. It’s only $1$ away. We can use that.
When we add $17+9$, what we’re really saying is that we’re going to take a group of $17$ of something and a group of $9$ of that same type of thing and shove them all into one big group. The addition problem asks how many of that thing are in the new group.
Since we’re going to shove them all together anyway, what if we took one item from the $17$ group and stuck it into the $9$ group before we shove them together. In other words, we make the two starting groups size $17-1=16$ and $9+1=10$. I mean they’re all going to be mixed up in the end anyway, so let’s just mix them up a bit now to make our lives easier. We still have the same total number of things. This is key. If we changed the overall total number of things, we would change the whole problem. But all we did was move the same things between the groups. We regrouped the very same items we started with, so we didn’t change the total.
But now we have an easier addition problem, because it has a zero in it! $16+10$. Adding the $10$s column, we see there are $2$ tens — or $20$ — and adding the $1$s column, we see there are $6$ ones. $20+6=26$. (Is that what those of you got who did the problem right away? Are you checking our work?)
Maybe instead of regrouping the way we did, you noticed that $17$ is close to $20$. It’s $3$ units away. We could use that instead: Take $3$ things from the $9$ group and move them into the $17$ group to make two new groups of $17+3=20$ and $9-3=6$. We then have $20+6=26$ again!
We can do this with larger numbers, too. $204+178$ is the same as $200+182$ if we take $4$ things from the $204$ group and put them in the $178$ group instead. Or $2041+1780$ can become $2021+1800$ if we take $20$ from the $2041$ group and put them in the $1780$ group.
What is regrouping?
With the strategy above, we avoid carrying. However, we still relied on the broader idea of regrouping. As the article Grouping and Regrouping in Math defines them, grouping and regrouping are the processes of combining and recombining items in ways that make it either easier or more useful to use, interpret, or communicate how many there are.
Grouping and regrouping are the processes of combining and recombining items in ways that make it either easier or more useful to use, interpret, or communicate how many there are.
Grouping and Regrouping in Math
In this case, since we were just going to smoosh all the “things” together into one group eventually anyway, we changed which group some of them started in, or regrouped those items, before performing the addition.
It is very important that regrouping never change the overall amount or number of items. In addition here it works because we simply moved the very same from one group to another: subtracting the same number from one addend (number being added) that we add to the other.
If we work only in symbols instead of thinking about the numbers as how many things, we can think of this subtracting-and-adding regrouping process as “adding zero” but making that zero look a certain way to make it more useful:
$204+178=178+204$ (I commuted these terms to avoid negative numbers)
$=178+0+204$ (since adding zero doesn’t change the overall sum)
$=178+(2-2)+204$ (I rewrote zero as the equivalent $2-2$)
$=178+2+204-2$ (I used the commutative property of addition)
$=(178+2)+(204-2)$ (I used the associative property of addition)
$=180+202=382$

(The astute among you might notice that I played a little fast and loose with those addition properties and the subtraction piece. I wanted to avoid negative numbers in this example, since those can sometimes intimidate folks. I converted “minus 2” to “plus negative 2” in my head to make these steps work. I promise that this made them legal moves even though associative and commutative don’t generally work or subtraction without taking this care.)
This adding zero that doesn’t quite look like a simple zero (here, adding $2-2$) is a tremendously useful skill in algebra. A variation (multiplying by a 1 that doesn’t quite look like a simple 1) also comes up in elementary school when learning to simplify, add, and multiply fractions.
I thought regrouping was just the new word for carrying
Carrying, it turns out, is one type of regrouping. Really, it and borrowing are both just shortcut notations for regrouping across place values. Regrouping is a much bigger idea than either carrying or borrowing. We saw just one use here. This idea of combining, un-combining, and recombining the groups represented by these numbers comes up again and again all throughout mathematics, from the earliest days of counting and simple addition through graduate and highly advanced mathematics. The more fluent students become with the process of regrouping, the more deeply we can expect they’ll understand topics such as fractions, arithmetic with negative numbers, and algebra. Carrying and borrowing, while part of the same phenomenon, just don’t bring the same depth of understanding or sense of numeracy.
Knowing Add-to-10 facts well makes this easy and fluid
Hopefully it became clear when we worked through examples that rapid knowledge of pairs of numbers that add to 10 is a great benefit in this method. The quicker you can recognize that $8+2=10$ or $70+30=100$ or $600+400=1000$, the quicker this method of addition becomes.
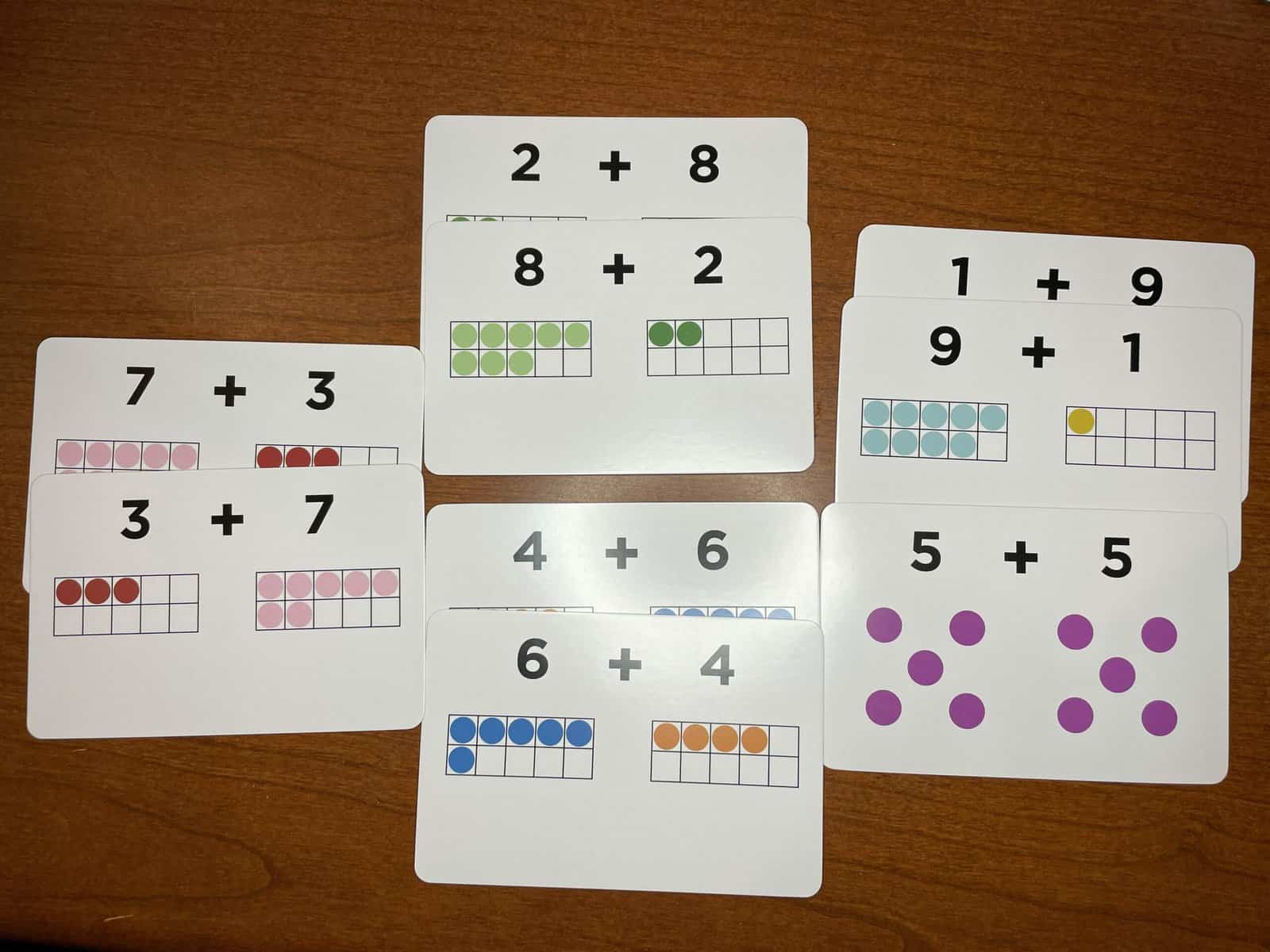

Most elementary curricula and classrooms now spend a significant amount of time working on add-to-10 facts, or number bonds to 10. A lot of the ways of representing numbers in school emphasize this as well, perhaps most notably, ten-frames. Extensive use of images such as ten-frames or manipulatives such as rekenreks help students internalize these facts without shame or stress and with truer understanding of what the facts represent.


Why didn’t we always learn this in school?
Consider the large shifts in technology as well as scientific pursuits over the past century or so, and what those shifts in technology have meant for our society’s mathematical needs.
Prior to the 1900s, the primary need for mathematics for most individuals was simple arithmetic. Tasks involved computing costs, keeping track of inventory or other items owned, and so forth. Those who couldn’t do mental arithmetic and estimating would have been easy to rip off. Paper may have been expensive and/or hard to come by. Thus, more involved computations needed a compact way of keeping track along the way. The “standard algorithms” evolved from this need as a shorthand means of keeping track of the various regrouping and other arithmetic steps. A lot of these new “numeracy” skills are actually quite old skills held commonly by folks throughout history. We have a couple of middle generations who did not specifically learn or develop these skills, but now we are bringing back some of these mental math and estimation skills.
Starting in the mid-1900s or so, we saw both paper become readily available as well as the Space Race. With the growing emphasis on science and technology, the pressure was on to do arithmetic fast and accurately. Mental math was less important since it was easier to find tools to write and record answers. The scientific endeavors used both much larger and much smaller numbers than most individuals in previous generations encountered. The focus in education became to grow more scientists, training children to do quick, accurate, and compact arithmetic. There was a focus on the algorithms that allowed arithmetic operations to be done quickly, accurately, and using as little space and materials as possible. It seems it was just assumed that learning to perform arithmetic would lead to an understanding of when and how to use the arithmetic, as well as the sense of numbers (numeracy) that underlay these operations. For some of us that worked. For others not. For a couple of generations, that a sense of numeracy was lost for too many students.
Today we carry high-powered calculators in our pockets. Most of the time, these machines can do the complicated arithmetic algorithms faster and more accurately than we can. However, a fluent human estimator and mental mathemagician will always be able to answer more quickly than you can even pull that calculator out of your pocket and hit the right buttons. It’s also important that we be able to evaluate the results these machines give us, both to interpret those results into real-world use and to notice and recognize when errors (such as typos) were made along the way. Thus, classroom focus returns now to numeracy, to mental math and estimation, and to knowing how the numbers work together and which arithmetic operations are appropriate for which scenarios.
So it’s not so much that schools never taught this, as instead the focus shifted toward rapidity for a couple of generations. Many of these skills are old strategies and approaches reimagined and taught directly to infuse confidence and competence in math for the technological world we live in and the needs of both society and individuals who live with that technology.
You’ve Got This!
