Regrouping is a fundamental mathematics practice. Deep, early understanding of what’s happening during regrouping will serve a student well in both math class and in daily life. But how do you explain this idea to someone else?
Explain regrouping by using physical tools and familiar contexts, such as blocks and money. Build the concept up through small but frequent interactions with the ideas in both the physical and the mental world.
The basic principles of regrouping may be simpler than you think. Grouping and regrouping goes back to the idea of taking things apart and putting them back together. In math, our decimal (ie, “by tens”) number system means breaking something into groups of ten or combining them into groups of ten. But children (and you!) have had grouping and regrouping experiences their entire lives. In fact, Grouping and Regrouping in Math examines an argument that grouping is the fundamental component of all of patterned and mathematical thinking, from the very beginnings of counting!
Use small and frequent interactions
Children especially learn best through play. They encounter ideas repeatedly in small and big ways, exploring them a little more deeply, stretching the concepts a little further each time. Classroom curricula are finally beginning to understand and embed this in their process, which is why you see a “spiral” effect of topics coming up over and over again, with ever so slight tweaks, grade after grade (learn more about spiral learning). Use this to your advantage. In this, as in so many other situations, we’re no longer expected to have “the big talk” with our children, but rather small exposures to the ideas at age-appropriate levels.
Use physical tools
Children can begin to absorb the basic principles of regrouping even before they can talk. Small children can learn, for example, that for a certain set of blocks, one long block is the same height as three small cubes. Or that one 4×2 duplo can completely and exactly cover two 2×2 duplos.
Preschoolers and early elementary children can cut shapes apart and put them back together again. They can pour and combine measuring cups of water to combine 4 quarter-cups into 1 full-cup. (There are even some bath toys built with these kinds of additive combinations in mind, where cup 1+cup 2 = cup 3, etc.)
Middle and upper elementary children can continue to explore with more advanced block systems such as Lego. They start learning about money and denominations. Have your child “make change” by trading 10 pennies in for 1 dime, or splitting 1 dollar into 10 dimes, etc. (Nothing motivates my tween daughter like money for Pokemon cards.)
Once children are familiar with the money system, you can introduce regrouping in the decimal system by limiting them to only pennies, dimes, dollars, 10-dollar bills, 100-dollar bills, 1000-dollar bills, etc. As you move into adding and problem solving, you can also invest in some base-10 blocks to model different situations. (Or just continue using your pennies and dimes and dollars to model.)
Use online tools
There are free online versions of several of the items above. For example, the tools at polypad.org allow you to “split” (ungroup) and “combine” (group) base-10 blocks as well as currencies (not just US currency). Their tools mix and match as well, making their number cards, their base-10 blocks, and their algebra tiles (for upper grades) work together extremely nicely.
If you’re looking for a different type of approach, check out Exploding Dots by James Tanton. You or your child will practice grouping, ungrouping, and regrouping not just in base 10 (decimal) system, but in a variety of different bases. The early activities are powerful for learning about these actions. The activities build insight not only into how place values and (re)grouping work, but also what it means to add, subtract, multiply, divide, and work with negative numbers. Using these mechanisms, James even gets into deep, unsolved advanced math problems without ever dealing with higher levels of mathematical classwork.
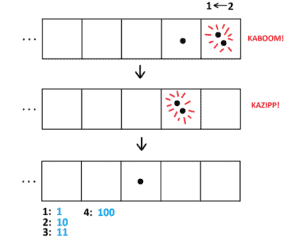
Bridge from activities to paper problems
Eventually, your child will need to move away from the physical manipulatives to performing the regrouping activities on paper. Wean them off. It is good for all learners to have a small amount of struggle; it encourages growth and is the only way to learn new things well. In education, we call this productive struggle. You can recognize productive struggle as problem solving, trying strategies, talking through ideas, and so forth. You know your child, though. Just before that moment when productive struggle turns unproductive, just before your child turns to negative self talk or throws their hands up, pull those physical or digital tools back out and let them use the tools again.
Learning is not linear. It’s not even uni-directional. We like to think that we consistently get better and better when we learn things, but sometimes we take steps back. That does not mean we’re not learning. It just means we still need to be supported at times to continue moving forward.
Meet your child where they are. Encourage them to think about the tools, even when they don’t have them, whenever it helps them. They can use tally marks or circles on the page to keep track as they picture the blocks or coins. (This is a great way to “show your thinking!”) Perhaps encourage them to use tally marks as units and then circle groups of 10 as a physical demonstration of literally grouping those 10 tally marks together. They count the number of circles for the tens place and the number of uncircled marks for the units place.
Believe it or not, this bridge building will build both their confidence and their skill until one day they’ll no longer need it. And more than that, they’ll be set up for deeper understanding of the mathematics to come.
Above all, remember to play, to experiment with math and the tools your child’s teacher introduces, and that learning is meant to be an enjoyable activity.
You’ve Got This!
