(Click here to read this post in English.)
Los mosaicos algebraicos puede ser extremadamente útil para desarrollar el pensamiento algebraico temprano y modelar ciertos tipos de problemas. Sin embargo, tienen limitaciones muy definidas y deben dejarse atrás en cierto punto del proceso de aprendizaje.
Los mosaicos algebraicos están limitadas por su naturaleza bidimensional para modelar polinomios de segundo grado o inferiores. Su naturaleza física también limita la cantidad de variables que pueden aparecer en los polinomios que modelan, así como la profundidad de comprensión de la negación y la resta.
Los mosaicos algebraicos están limitadas por su dimensionalidad. Usando solo dos dimensiones, los mosaicos algebraicos limita al profesor y al estudiante de álgebra a polinomios de segundo grado (cuadráticos) o inferiores (líneas o constantes). En segundo lugar, solo algunos conjuntos de los mosaicos algebraicos vienen con más de una variable y casi nunca con más de dos variables, lo que limita aún más los polinomios que pueden modelar. Además, cuando se introducen los coeficientes negativos y la resta, la interpretación física de los mosaicos algebraicos como área se vuelve sospechosa por dos razones: 1) el área no puede ser negativa y 2) $x^2-3x$ no debe cubrir la misma cantidad de área como $x^2+3x$, sin embargo, en mosaicos algebraicos, lo hacen. Siempre que no se use con cuidado el lenguaje en torno a las fichas “negativas”, los mosaicos algebraicos también pueden exacerbar los malentendidos acerca de si $-x$ es siempre negativo. Finalmente, los mosaicos algebraicos, como muchos manipulativos, si bien son excelentes para desarrollar la comprensión y poder visualizar e interpretar, también pueden volverse engorrosas y menos eficientes que otros métodos para realizar manipulaciones algebraicas.
¿Cómo puedes superar estos? No abandones los mosaicos por completo. En cambio, siempre use los mosaicos simultáneamente con las manipulaciones simbólicas. Utilice ambos al principio y asegúrese de comprender cada paso de las representaciones simbólicas. Gradualmente haga la transición a usar cada vez menos los mosaicos y cada vez más las estrategias simbólicas. Exploremos cada una de estas limitaciones para que entendamos por qué esto es importante.
Esta publicación se publicó originalmente en mathteacherbarbie.com. Si lo estás leyendo en otro lugar, estás leyendo una copia robada.
Las dos dimensiones limitan los polinomios que se pueden modelar
Es posible que ya hayas notado que los mosaicos algebraicos “más grandes” representan $x^2$ (o tal vez la ficha $xy$ o $y^2$ si tienes la suerte de tener un conjunto con una segunda variable). Para expandirnos aún más a $x^3$, necesitaríamos tratar con cubos de álgebra tridimensionales, no con mosaicos 2D. Sin esa tercera dimensión, estamos atascados con polinomios de segundo grado (cuadráticos) o inferiores. Por lo tanto, los mosaicos algebraicos no nos ayudarán cuando tengamos términos con $x^3$ o potencias superiores.
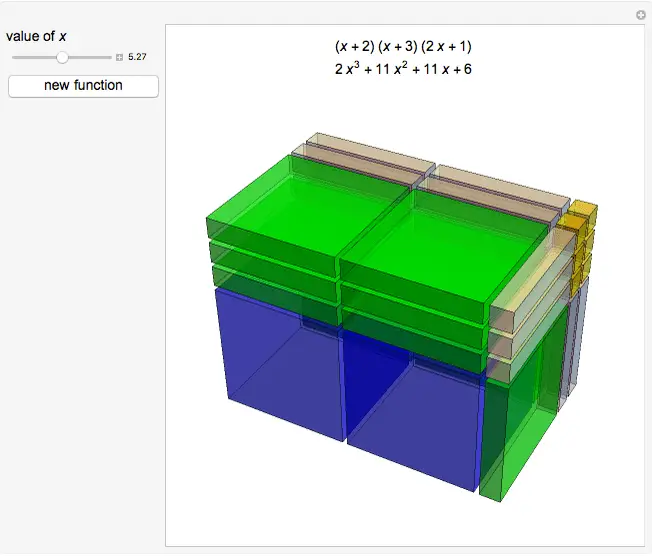
David L. Srebnick
“3D Algebra Blocks”
http://demonstrations.wolfram.com/3DAlgebraBlocks/
Wolfram Demonstrations Project
Publicado: July 2 2014
La falta de variables limita los polinomios que se pueden modelar
Si tiene suerte, su conjunto de fichas puede tener una segunda variable (longitud de lado desconocida). Casi ninguno tendrá más de 2. Los mosaicos algebraicos se limitan a representar polinomios con solo el número de variables que tienen longitudes de lado desconocidas, generalmente solo una variable, a veces dos.
La introducción de mosaicos “negativos” desequilibra la interpretación del área
Existen múltiples problemas con los mosaicos algebraicos como área cubierta cuando introducimos coeficientes negativos y restas. Dado que el área en este contexto mide una longitud física multiplicada por el ancho, y dado que la longitud y el ancho nunca serán negativos, toda la idea del área negativa rompe las reglas de medición. Incluso si pensáramos en estos coeficientes negativos como un tipo de resta de “quitar”, en realidad no quitamos usando mosaicos algebraicos. En cambio, parece que sumamos de la misma manera que lo haríamos si el coeficiente fuera positivo, solo que con un color contrastante. Lo que conduce a polinomios con coeficientes opuestos que cubren la misma área.
Los mosaicos “negativos” pueden reforzar los malentendidos del signo de $-x$
Si somos perezosos con el lenguaje, lo que sucede a menudo, los estudiantes suelen tener la idea errónea de que $-x$ siempre es un número negativo. Pero este no es el caso. $x$ puede tomar valores positivos o negativos. $-x$ siempre debe leerse como “lo opuesto de”. Por tanto, si $x$ era positivo, entonces $-x$ es negativo (lo opuesto de positivo). Pero siempre que $x$ tome un valor negativo, entonces $-x$ será lo contrario: positivo. Este es un malentendido común, reforzado por el lenguaje casual (y erróneo) “negativo”. Los mosaicos algebraicos se pueden usar para reforzar cualquiera de las interpretaciones, y se debe tener cuidado para saber cómo se usan las fichas “negativas”.
Los mosaicos algebraicos pueden ser engorrosos e ineficientes
Nunca querrá depender tanto de una herramienta que se convierta en una muleta. Usa los mosaicos algebraicos para ganar comprensión, pero no descuides las manipulaciones simbólicas. Practíquelos, ya que en última instancia serán más rápidos, más eficientes, tendrán una gama más amplia de usos (como polinomios de mayor grado) y estarán más disponibles incluso cuando no tenga acceso a los mosaicos. Usa los mosaicos para entender, pero no dejes que te detengan. Y sobre todo, recuerda…
¡Sí que está a tu alcance!
