(Click aqui para leer este articulo en español.)
Algebra Tiles can be extremely useful in developing early algebraic thinking and modeling certain types of problems. However, they have very definite limitations and should be left behind at a certain point in the learning process.
Algebra tiles are limited by their 2-dimensional nature to modeling second degree or lower polynomials. Their physical nature also limits the number of variables that can appear in polynomials they model as well as the depth of understanding of negation and subtraction.
Algebra Tiles are limited by their dimensionality. Using only two dimensions, Algebra Tiles limit the algebra teacher and student to second-degree (quadratic) or lower (lines or constants) polynomials. Secondly, only some sets of algebra tiles come with more than one variable, and almost never with more than two variables, further limiting the polynomials they can model. Further, once negative coefficients and subtraction are introduced, the physical interpretation of algebra tiles as area becomes suspicious for two reasons: 1) Area can’t be negative, and 2) $x^2-3x$ should not cover the same amount of area as $x^2+3x$, yet in algebra tiles, they do. Whenever language around the “negative” tiles is not carefully used, algebra tiles can also exacerbate misunderstandings around whether $-x$ is always negative. Finally, algebra tiles, as many manipulatives, while great for building understanding and being able to envision and interpret, can also become cumbersome and less efficient than other methods of performing algebraic manipulations.
How can you overcome these? Don’t abandon the tiles altogether. Instead, always use the tiles simultaneously with the symbolic manipulations. Use both at first, and make sure you understand each step of the symbolic representations. Gradually transition to using the tiles less and less and the symbolic strategies more and more. Let’s explore each of these limitations so that we understand why this is important.
This post contains affiliate links. If you purchase through these links, I may earn a small commission at no additional cost to you. You can read more about how I choose affiliates and products at my affiliate page.
Two Dimensions Limit Polynomials That Can Be Modeled
You may have noticed already that the “biggest” algebra tiles represent $x^2$ (or maybe the $xy$ or $y^2$ tile if you’re lucky enough to have a set with a second variable). In order to expand further to $x^3$, we would need to deal with 3-dimensional algebra cubes, not 2D tiles. Without that third dimension, we are stuck with second-degree (quadratic) or lower polynomials. Thus, the algebra tiles (affiliate link) won’t help us when we have any terms with $x^3$ or higher powers.
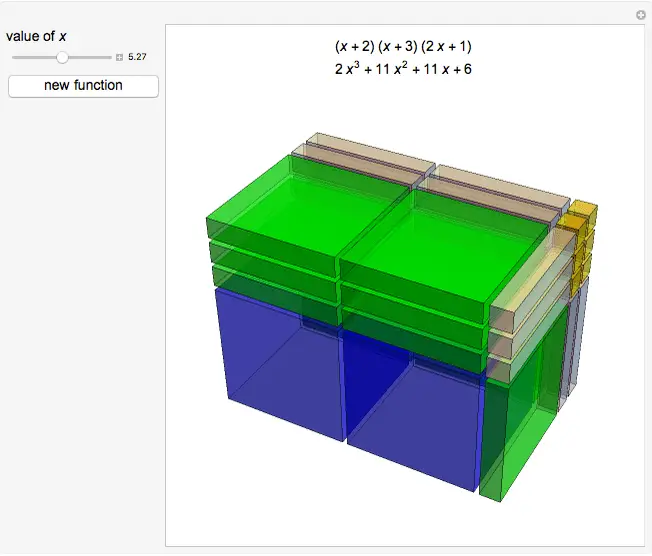
David L. Srebnick
“3D Algebra Blocks”
http://demonstrations.wolfram.com/3DAlgebraBlocks/
Wolfram Demonstrations Project
Published: July 2 2014
Lack of Variables Limit Polynomials That Can Be Modeled
If you’re lucky, your set of tiles might have a second variable (unknown side length). Almost none will have more than 2. Algebra Tiles are limited to representing polynomials with only the number of variables that they have unknown side lengths — usually just one variable, sometimes two.
Introducing “Negative” Tiles Throws Off Area Interpretation
There are multiple problems with reading the algebra tiles as area covered when we introduce negative coefficients and subtraction. Since area in this context measures a physical length times width, and since length and width won’t ever be negative, the whole idea of negative area breaks the rules of measurement. Even if we thought of these negative coefficients as a “taking away” kind of subtraction, we don’t actually take away using the algebra tiles. Instead, we appear to add the same way we would if the coefficient was positive, just with a contrasting color instead. Which leads polynomials with opposite coefficients to cover the same area.
“Negative” Tiles May Reinforce Misunderstandings of Sign of $-x$
If we are at all lazy with language, which often happens, students frequently gain a misconception that $-x$ is always a negative number. But this isn’t the case. $x$ might take on either positive or negative values. $-x$ should always be read as “the opposite of $x$.” Thus, if $x$ was positive, then $-x$ is negative (opposite of positive). But whenever $x$ takes on a negative value, then $-x$ will be the opposite: positive. This is a common misunderstanding, reinforced by the casual (and wrong) language “negative $x$.” Algebra tiles could be used to reinforce either interpretation, and care must be taken to know how the “negative” tiles are being used.
Algebra Tiles Can be Cumbersome and Inefficient
You never want to rely so heavily on a tool that it becomes a crutch. Use algebra tiles to gain understanding, but don’t neglect the symbolic manipulations. Practice those, as ultimately they will be quicker, more efficient, have a wider range of uses (such as higher degree polynomials), and be more readily available even when you don’t have access to the tiles. Use the tiles to understand, but don’t let them hold you back. And above all, remember…
You’ve Got This!
