Students are taught multiple models in mathematics. This gives them multiple opportunities to understand an idea, strengthens and deepens connections to the material, and provides multiple tools for problem solving. One principal model for multiplication is the area model. This model of multiplication grows with the students into algebra and potentially beyond, so it serves students well to anchor their understanding of this model. But how do we even start with this model?
An area model allows us to keep track of multiplication visually by placing each pairwise multiplication of single digit place values into a grid that is later added together.
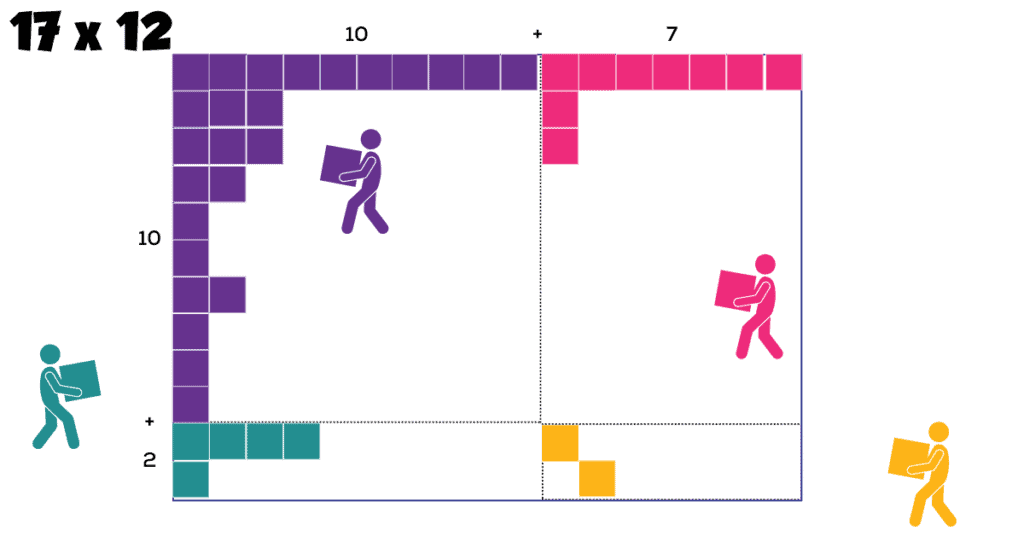
To set up an area model, start with the multi-digit numbers to be multiplied and expand them into their place value expansions. Draw a rectangle. Along the top of the rectangle, write the expanded form of the first number being multiplied; stretch the expanded form along the whole top of the rectangle. Along the left side, write the expanded form of the second number; make sure the first number is near the top of the side and the last is near the bottom and any others in the expansion are distributed along the side in between. Draw a vertical line down from every plus sign along the top edge, and draw a horizontal line across from every plus sign along the side to create a grid of smaller rectangles. Then multiply within each smaller rectangle according to the place value numbers in each direction. Finally, add up all of the results inside the rectangle and report the result.
Read on below for more information about each of these steps. You can also watch all of the steps in action at the Math Teacher Barbie video Using the Area Model to Multiply Larger Numbers.
This post was originally published on mathteacherbarbie.com. If you are viewing this elsewhere, you are viewing a stolen version.
Expand multi-digit numbers into place value expansions
As described in the post Grouping and Regrouping in Math and the video Place Value as Grouping, our number system is built to use only a reasonable number of symbols by using place value to represent groups. If, for the moment, we ignore place values to the right of the decimal (fractional place values), then the rightmost numeral represents the number of units, or 1s that are left over after splitting out the larger groups. The second-from-right numeral represents the number of tens (10s). The third-from-right numeral represents the number of hundreds (100s). And so on. We expand a multi-digit number when we explicitly call out what each place value means. For example, in the number 2,346,
- the numeral 2 represents 2 thousands, or 2,000
- the numeral 3 represents 3 hundreds, or 300
- the numeral 4 represents 4 tens, or 40 (say “four tens” many times in a row and rapidly, and eventually you may hear how “four-tens” evolved over time to be “forty”)
- the numeral 6 represents 6 ones, or just 6.
So the whole number 2,346 can be expanded as $2000+300+40+6$.
Each of the two numbers you’re multiplying together is called a factor in that multiplication problem. Expand each factor this way into its place value expansions.
Some numbers will have a zero in them. While it won’t necessarily ruin the process if you don’t, it’s usually best to still write out that part of the expansion. For example, best practice would have you expand 709 as $700 + 0 + 9$, with the 0 representing zero tens.
Draw a rectangle and label the edges
Now draw a large-enough rectangle. How large is large enough? That depends on your handwriting. You’re going to split that rectangle up into somewhere between 4 and a dozen or so smaller squares (more than that, and the area model is no longer a great way to multiply because it’s so large). In each of these smaller squares, you’re going to need to write a number. Make your rectangle large enough that you can write lots of numbers inside.
Then label the top and the left sides with their respective factors, in expanded form. Starting with the largest number in the expansion, label each section along the top with an addend from the expanded form, spacing the expanded terms and plus signs all along the top edge. Along the left side, starting with the largest number in the expansion of the second factor, write each expanded term or plus sign on a separate line, stretching from the top of the rectangle to the bottom.
Divide the rectangle
Starting just below each plus sign along the top, draw a vertical line down all through the rectangle to split it into smaller rectangles. Then starting just to the right of each plus sign along the left, draw a horizontal line across the rectangle to further split it into even smaller rectangles.
Multiply within each small rectangle
Put your finger in any of the smaller rectangles. If you move your finger straight up the page, you should find one number. If you move your finger left on the page from that small rectangle, you should find another number. Multiply those numbers. These should be easier to multiply because they should have lots of zeros. Do this for each of the small rectangles.
Add up the insides and report the result
Finally, add up all the little rectangles inside. They should be relatively easy to add because a) addition is a lower-level skill than multiplication, and b) there are lots of zeros. Once you finish adding up the little rectangles, you have your answer to the original multiplication problem! If you’re allowed to, check your work with a calculator or another method, and give yourself a pat on the back for working all the way through it! And then another pat on the back because…
You’ve Got This!
To explore even more about the Area Model, check out my Area Model Playlist at the Math Teacher Barbie YouTube channel.
