(Click here to read this post in English.)

Los problemas de palabras son la pesadilla de la existencia de los estudiantes de matemáticas. A veces podríamos resolver fácilmente exactamente el mismo problema si surgiera en la vida real, pero nos resultaría difícil cuando se presentara como un problema verbal. Tal vez sea la frase, la lectura o simplemente el miedo a equivocarse. Lo más probable es que la razón sea diferente para cada uno.
Se han propuesto muchas estrategias paso a paso para resolver problemas escritos y es posible que su hijo incluso esté aprendiendo una de ellas en clase. Parte de esas estrategias son listas de “traducciones” de palabras a operaciones, es decir, una lista de palabras “clave” o “pistas” para cada operación. Todo esto, sin embargo, puede fallarnos en un momento u otro. Entonces, ¿cómo sabemos de manera confiable si debemos sumar, restar, multiplicar o dividir en un problema escrito?
Para determinar qué operación usar en un problema escrito, observe la relación entre las diferentes cantidades. Por lo general, la suma o resta es mejor con grupos de diferentes tamaños. Elija multiplicación o división cuando todos los grupos sean del mismo tamaño o al escalar (hacer algo más grande o más pequeño sin cambiar su aspecto general o proporciones).
La suma o resta es útil cuando dos o más cantidades se pueden contar o combinar para formar un grupo más grande. Esto también se conoce como relación parte-parte-todo (o parte-parte-parte-todo, etc.). La multiplicación o división es útil cuando hay varios grupos del mismo tamaño que se combinan o se dividen. Estos se pueden combinar para obtener relaciones más complicadas (como contar una cierta cantidad de grupos de una cantidad y luego agregar una cantidad adicional a esa cantidad).
Esta publicación se publicó originalmente en mathteacherbarbie.com. Si lo está viendo en otro lugar, está viendo una copia robada.
Comience ignorando los números
¡En serio! Ignora los números. Lea el problema en voz alta. En lugar de leer un número, diga la palabra “algunos” o una palabra similar. ¿Tiene dos o más grupos combinados para crear otro grupo (suma) o un subgrupo extraído de un grupo más grande (resta)? ¿Estás ampliando o reduciendo algo, o haciendo una cierta cantidad de copias de un grupo (multiplicación), o dividiendo una cantidad en grupos iguales más pequeños (división)?
Preescribe la respuesta
Concéntrese en lo que el problema le pide encontrar. Vuelva a redactar la pregunta o afirmación en una respuesta de oración completa, dejando los números en blanco (si le ayuda, escriba la palabra “algunos” donde podría ir un número). Esto no sólo le brindará una excelente configuración cuando llegue al final del problema, sino que también puede ser extremadamente útil para ayudarlo a descubrir el contexto del problema.
La mayoría de los problemas del mundo real comienzan con la pregunta primero (necesito saber ___, o me pregunto ), y tenemos que buscar la información para responder. A menudo somos bastante buenos en esto. Los problemas escritos en la clase de matemáticas tienden a darnos primero la información y luego la pregunta. Esto puede ser parte de lo que resulta abrumador. Dale la vuelta y concéntrate primero en el objetivo, y de repente descubrirás que tienes mucha más información de la que pensabas.
Utilice números más simples para descubrir relaciones
A medida que comience a comprender el contexto, comience a traer los números nuevamente. Si los números son grandes, fraccionarios o decimales, considere fingir temporalmente que los números son mucho más pequeños. Lee el problema, pero sustituye números enteros, el tipo de número que podría ser el Número del Día de Sesame Street, hasta que descubras qué operaciones y relaciones existen. (¡Entonces asegúrate de volver a colocar los números originales en su lugar!)
Decide qué tipos de relaciones tienen tus cantidades
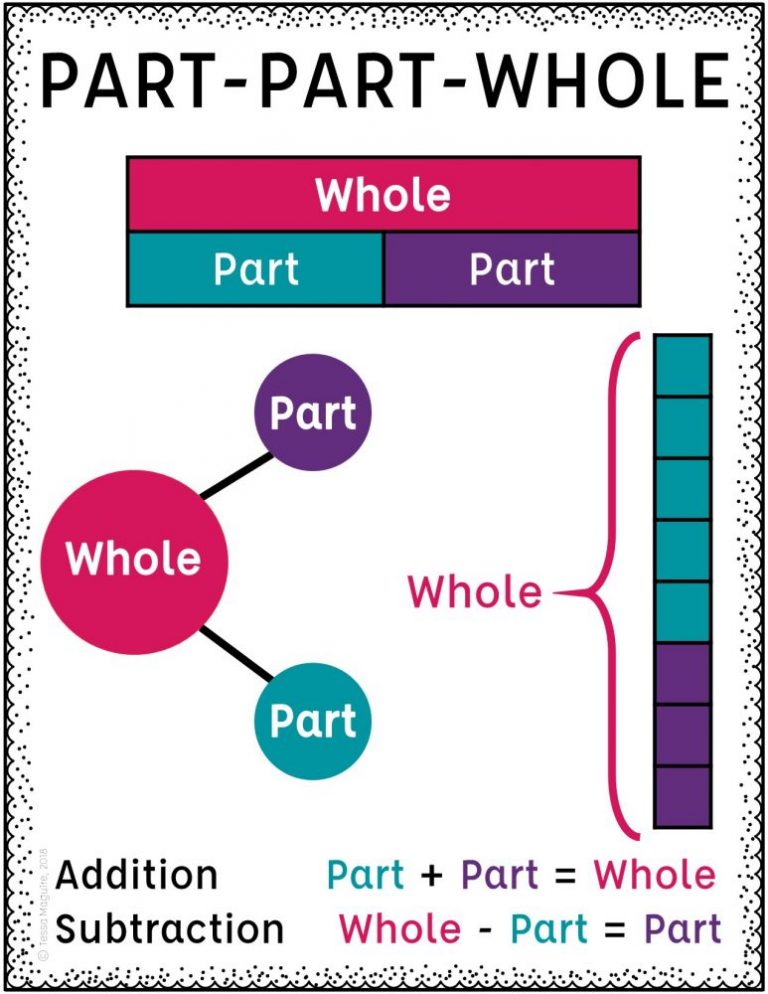
Si sigue los pasos anteriores y aún no ve las relaciones, considere lo siguiente:
- Suma: si tienes más de una parte que forma un todo y quieres saber sobre el todo, probablemente te encuentres en un escenario de suma. Los planes de estudio de primaria a menudo llaman a esto una relación parte-parte-todo. Todas las “palabras clave” de la suma indican este tipo de relación:
- total o suma de las partes
- una parte más que o incrementada en otra parte
- todas las partes juntas, en total, combinadas
- etc.
- Resta: La resta también implica una relación parte-parte-todo, pero esta vez quieres conocer una de las partes.
- cuántos había en la parte que quitasteis; cuántos más que la parte restante tenías
- cuál es la diferencia entre el todo y la parte restante
- cuánto menos tienes en la parte restante de lo que había en el total
- Multiplicación: La multiplicación puede repetirse en grupos de igual tamaño o escalarse hacia arriba (números mayores que uno) o hacia abajo (fracciones entre 0 y 1) proporcionalmente.
- División: La división también se ocupa de grupos repetidos de igual tamaño o escala. Sin embargo, la división responde con el número de grupos o con el tamaño de cada grupo (mientras que la multiplicación responde con el total de todos los grupos). Si bien puedes usar la división para aumentar o reducir la escala, una vez que aprendes a usar fracciones, suele ser más fácil pensar en todas las escalas como una multiplicación.
Muchas estrategias de problemas escritos enseñan principalmente listas de “palabras clave”, como las que aparecen en cursiva arriba. Existen tres problemas al depender de esta estrategia:
- Las listas de palabras clave son realmente difíciles de memorizar.
- Ninguna lista de palabras clave está completa.
- ¡Varias palabras clave (como más que) aparecen en varias listas!
Por eso centrarse en las relaciones entre cantidades es más fiable que las listas de palabras clave.
Combine las operaciones según sea necesario
Si ve más de uno de estos tipos de relaciones, es posible que necesite utilizar más de una operación. Por ejemplo, es posible que tengas una parte de una parte-parte-todo que a su vez esté formada por grupos del mismo tamaño, lo que significaría combinar la suma y la multiplicación. O puede descubrir que le quitaron una parte y la parte restante se dividió en grupos iguales: ¡resta y división! Quita la atención de los números, busca las relaciones entre los sustantivos del problema, no las cantidades, y elige tus operaciones con confianza y con muchas menos conjeturas.
¡Sí que está a tu alcance!
