Algebra tiles are arguably the most common and useful manipulative in the algebra classroom. They are also one of the most misunderstood. Advocates are wholehearted and love to show off the exciting things they are able to demonstrate and teach using the tiles. However, in their enthusiasm, these same individuals forget the basic learning they had to do to use the tiles effectively in the first place. This was my own experience of learning to use algebra tiles. I’d like to save you some of that headache here so you can participate more fully in the wonder and enthusiasm.
Algebra tiles are a physical manifestation of the area model of multiplication as applied to unknown variable lengths. Individual tiles represent individual terms, and collecting tiles together is equivalent to combining like terms and adding expressions in algebra. Multiplication (and thus factoring) of expressions can be interpreted as further applying the area model. (In fact, algebra tiles are extremely useful in tying the technique of completing the square to its name.)
However, being physical manifestations, algebra tiles are also limited by 2-dimensional physics, thus limiting their useful life. This can be used as both a strength and a weakness of the tiles — forcing teachers to build the symbolic manipulations alongside and preventing the tiles from becoming too much of a “crutch” to learning.
This post was originally published on mathteacherbarbie.com. If you are reading it somewhere else, you are reading a stolen version.
What are algebra tiles?
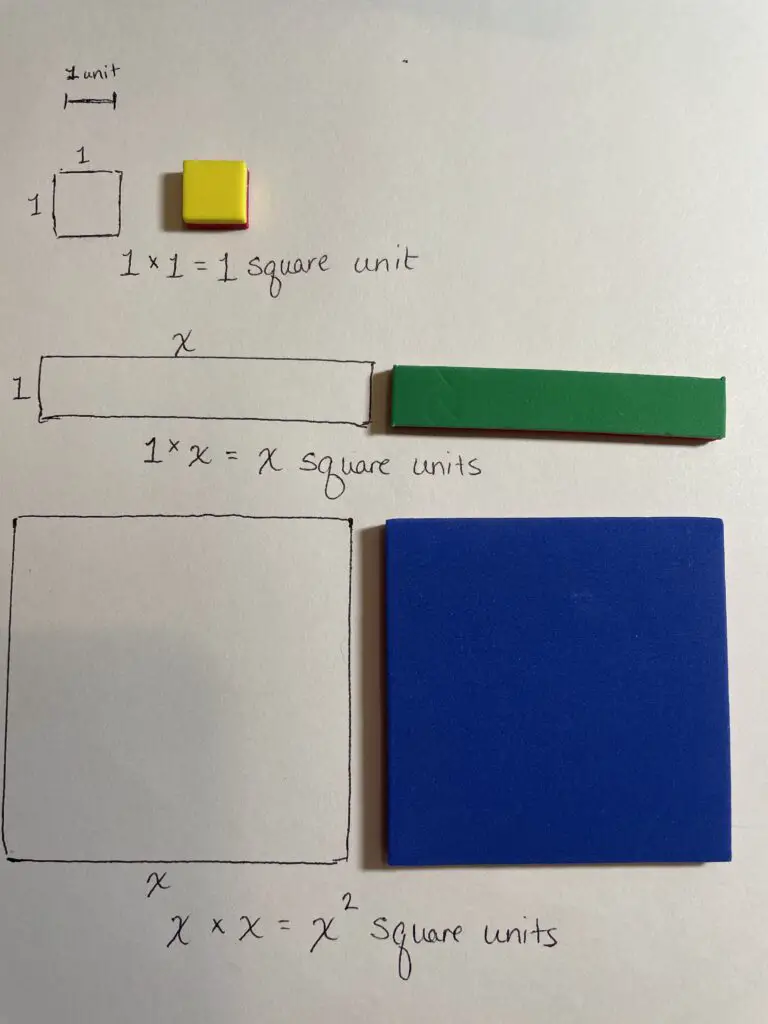
Algebra tiles are a collection of flat blocks (or “tiles”) with different combinations of edge lengths. All algebra tiles sets will have a smaller edge length which is thought of as length 1 unit and a longer edge length which is thought of as length $x$. Length $x$ is always meant to be an unknown, unspecific length, (and should never be a multiple of length 1, which can lead to false conclusions and understandings).
In all algebra tile sets, you will find small squares that are 1-by-1, long rectangles that are 1-by-$x$, and larger squares that are $x$-by-$x$.
Some tile sets have a different unknown (unmeasured) side length $y$ with various combinations of tiles incorporating that side length as well. Some come double-sided with a different color on each side to represent negatives vs positives.
Algebra tiles are a physical representation of algebraic expressions, based on the same ideas as the area model of multiplication. Specifically, the individual tiles each represent individual terms of the expression according to the area they cover:
- 1-by-1 tile represents “+1” (or “-1” if the negative color is used)
- 1-by-$x$ tile represents “+$x$” (or “-$x$” if the negative color is used)
- $x$-by-$x$ tile represents “+$x^2$” (or “-$x^2$”…)
- 1-by-$y$ tile represents “+$y$”
- $y$-by-$y$ tile represents “+$y^2$”
- $x$-by-$y$ tile represents “+$xy$”
Placing multiple algebra tiles together corresponds to building an algebraic expression from these various terms.
How are algebra tiles best used?
Algebra tiles are most useful early in the process of understanding algebraic concepts such as terms, combining like terms, and basic expression arithmetic. They then become useful once again at the beginning of factoring. They do have significant limitations preventing much use beyond this scope. However, many students will find extremely useful the opportunity to learn kinesthetically and interpret basic algebraic expressions physically. Others will find the visual images useful. Personally, I expect this usefulness to only increase with the increased use of the area model in late elementary school.
In my classroom, I pull out the algebra tiles as soon as I introduce the idea of a variable. I start with the 1-by-1 tile to set my “unit” edge length, defining the length of one side of that small square as “1” and discussing how it covers “1 square unit” of area. I add one or more of the small squares and ask how much area they now cover all together.
I then introduce the 1-by-$x$ tile and ask how much area it covers. After brief discussion (with maybe some haphazard, hand-wavy attempts to figure out precisely how many units the $x$ length is, but never carefully detailing it), I lead the conclusion that we do not know precisely how long the rectangle is and I introduce $x$ to represent its length. We then define the area of that rectangle to be $x\times 1$ or $x$ square units. Adding a few more rectangles, we can start to see the idea of $2x$ and $3x$, etc, emerge for the students.
Then we can start to introduce combinations of 1 and $x$ tiles as well as introducing the $x^2$ tile when the students are ready (this latter varies by group). This is a great time to give students algebra tiles and ask them to model various expressions using the tiles and to interpret various tile setups into algebraic expressions. I find that for both students and teachers who are new to algebra tiles, this is a critical step. (It is, unfortunately, a step that my own introduction to algebra tiles was missing. As a result, I spent many a professional development session at a loss wondering what in the world was going on around me.)
Finally, we have constructed algebraic ideas in our students’ brains and can give them the common language and definitions to discuss those ideas. Here’s where the students and I together define term, expression, combining like terms, etc.
With these basics in hand, the tiles become a tool for interpreting, exploring, discovering, and discussing a variety of algebraic operations in 2-dimensional space. They become part of the scaffolding of algebraic ideas. However, I recommend using them frequently but not constantly so that they do not become a crutch and to manage students’ ability to use algebra beyond the 2D limitations of the tiles.
For more information about the basics of using algebra tiles, check out my video: Algebra Tiles Basics.
Who benefits most from algebra tiles?
The same students who benefit most from visual models and kinesthetic learning will benefit from using algebra tiles. The tiles provide both a visual model as well as opportunities to move the tiles around and explore how different expressions are both the same and different.
Students who are skeptical about algebra may find the tiles useful. Often algebra comes across as a set of arbitrary rules to be memorized with no real meaning behind them. The tiles provide a physical meaning and interpretation of algebraic symbols, as well as the combinations thereof.
Students who struggle with definitions and terminology may find the tiles useful as concrete ideas to tie those words to.
Students who are intrigued by imagining higher dimensions may find the tiles useful. In particular, these students may find their imaginations piqued and their inventive spirit challenged by discussions of the limitations of algebra tiles as being “stuck” in the 2-dimensional plane. Even the leap to 3D “algebra blocks” introduces ideas of unwieldy exponential growth in how to physically represent all the possible combinations. Imagining what 4D or higher algebra blocks could be, how many variations a “set” of them would have, etc, could occupy the imaginations of many a student.
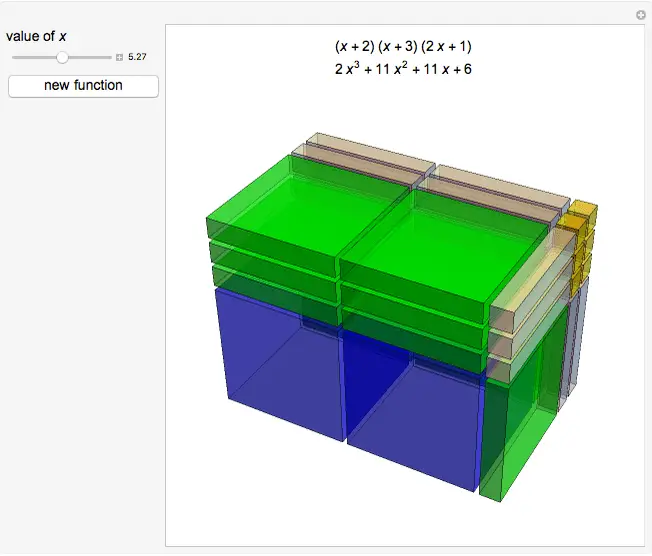
David L. Srebnick
“3D Algebra Blocks”
http://demonstrations.wolfram.com/3DAlgebraBlocks/
Wolfram Demonstrations Project
Published: July 2 2014
When to stop using algebra tiles
Honestly, algebra tiles are useful tools to have on hand at the drop of a hat. Rather than stopping, hopefully you will find yourself tapering off their use.
You may find limited use for algebra tiles when introducing negative/opposite/subtractive terms in expressions. Using the tiles to discuss “zero pairs” can be extremely useful. (This is especially true in virtual algebra tile sets where a tile and its opposite can visually be shown to cancel each other out. In fact, this may be a great point to switch from physical algebra tiles to the virtual tools in your classroom for this very reason.) However, the physical interpretations of algebra tiles as a representation of the area model begins to break down once we get very far into negative/opposite/subtractive terms. You may find that very concrete-thinking students begin to get confused by this relatively quickly.
Due to their limitations, algebra tiles also will not be useful for more than 2 variables (more than 1 variable in some sets) and expressions with degree higher than 2. Thus, your use of algebra tiles should always focus on scaffolding the abstract ideas so that students can do the operations symbolically without the tiles, easing their way into these concepts where the tiles just simply are not practical.
That said, I do find it useful to have them on hand to pull out occasionally and remind students of the basics as we learn to deal with more and more complex expressions. I also find them useful to pull out again for a day or two as we learn factoring, relating it back to the multiplication that is its inverse operation.
Listen to your students and their mastery and their struggles. Remember that the tiles have limitations and that the tiles are not a goal in and of themselves. Rather, the tiles are there as tools. Use them as such, and when they are no longer useful to you and your students, leave them in their box unless/until they become useful again.
You’ve Got This!
