
Those of us in school before the 2010s likely call it carrying the one. Those in school since then probably call it regrouping. Either way,
Carrying the one is the process of taking ten units, grouping them together, and writing them instead as one group in the next bigger place value. It is a result of using our base-10 number system, where each place value to the left represents 10 of the place on the right.
This post was originally published on mathteacherbarbie.com. If you are reading this elsewhere, you are reading a stolen version.
Carrying the one: 9+1 (ie, counting)
What happens when we have 9 of something and add one more? We call that number “ten.” Can you picture the number we would write? Are you picturing 10? In this case, we took our total of ten units (ten “ones”), grouped them together as a unit, and call it “one unit in the tens place and nothing left in the ones place,” or 10 (“one-zero”).
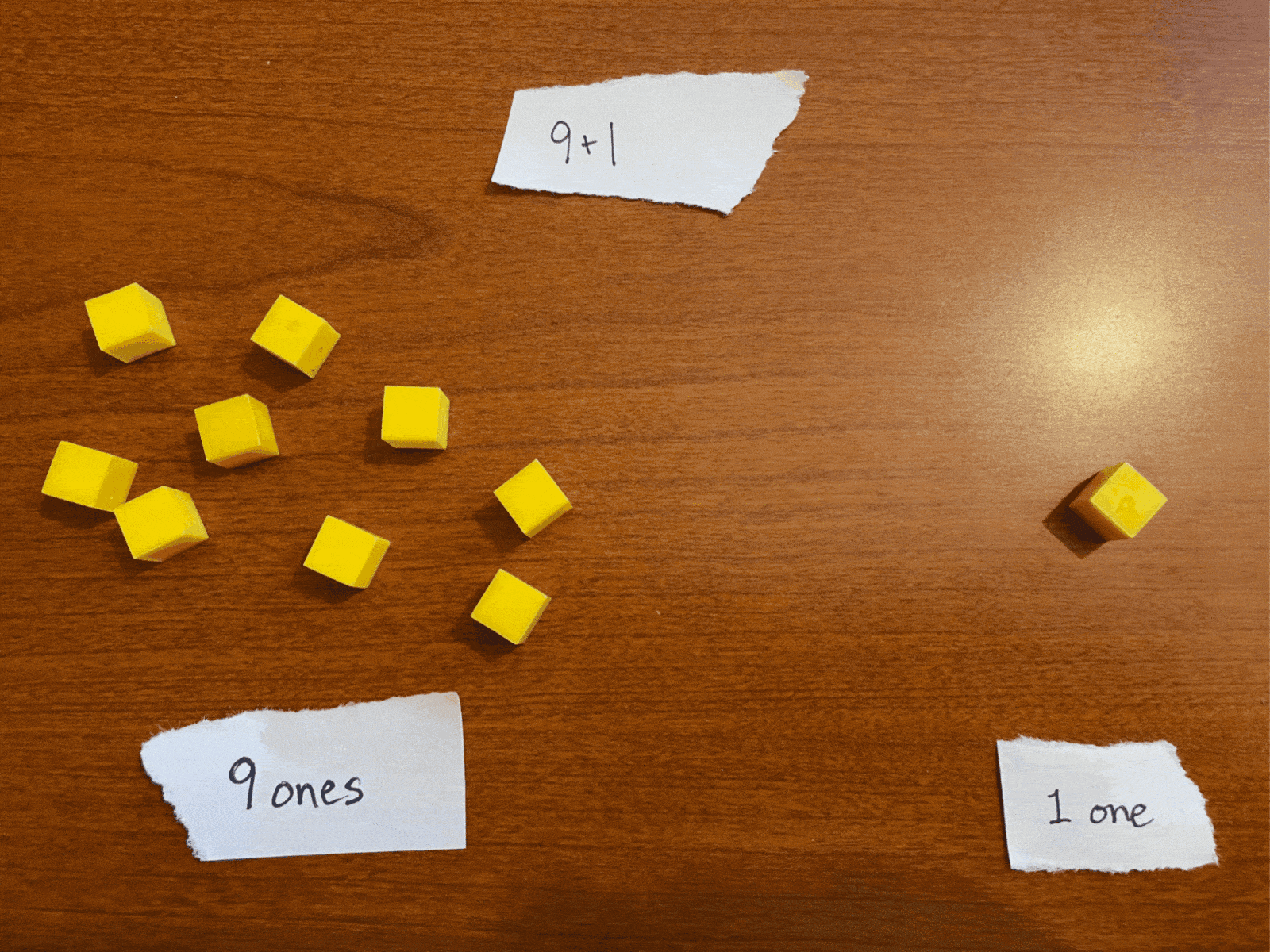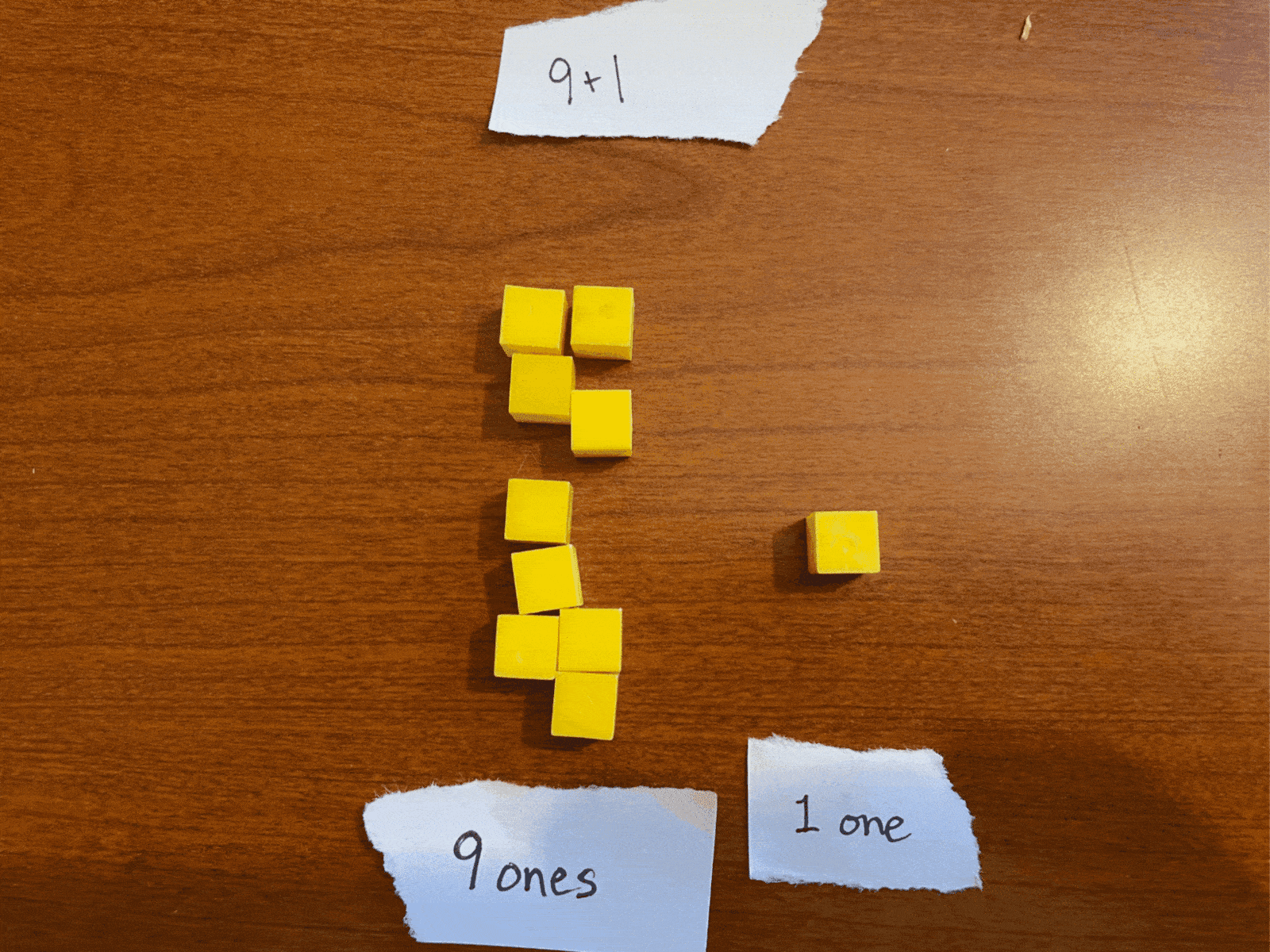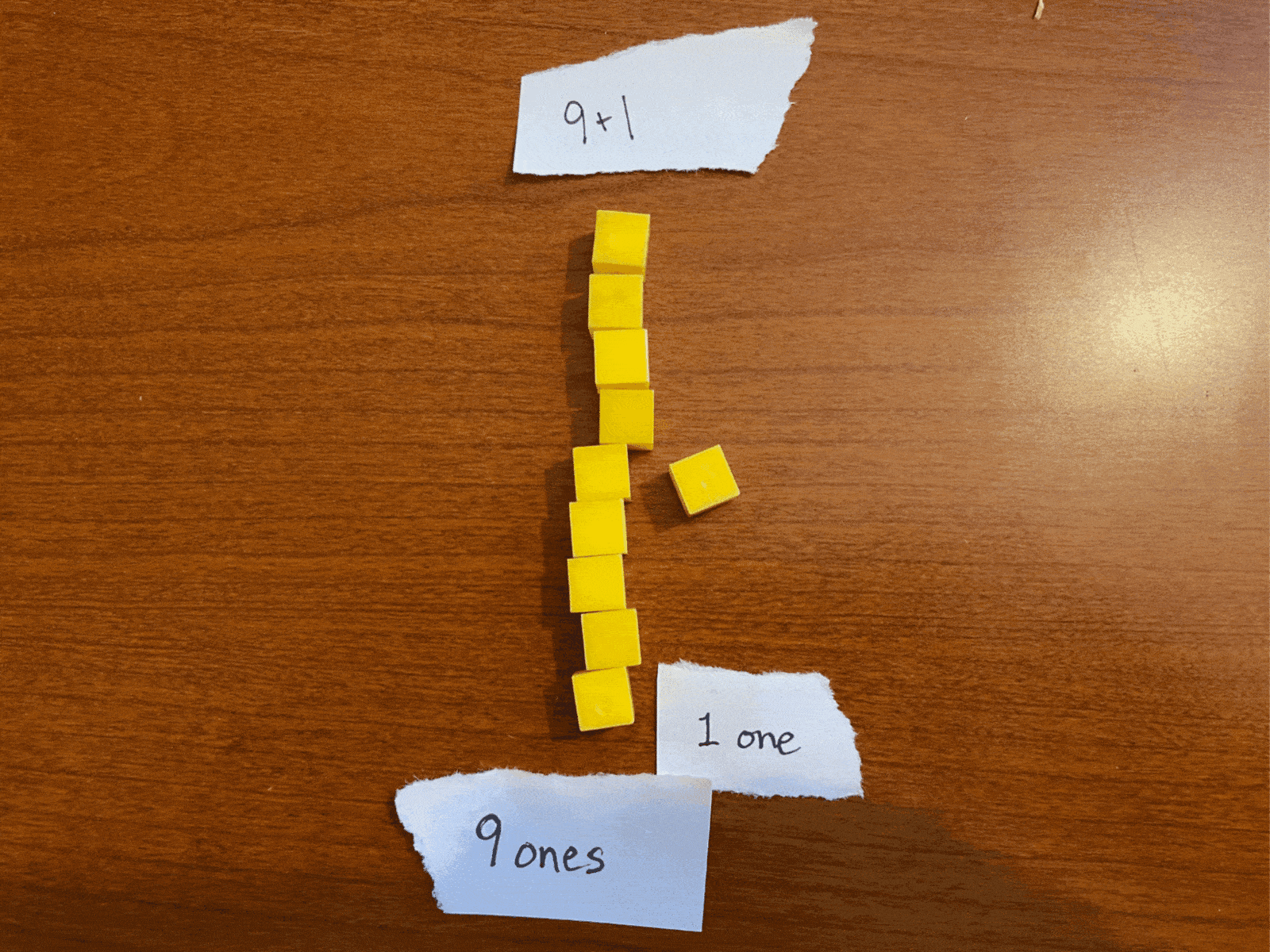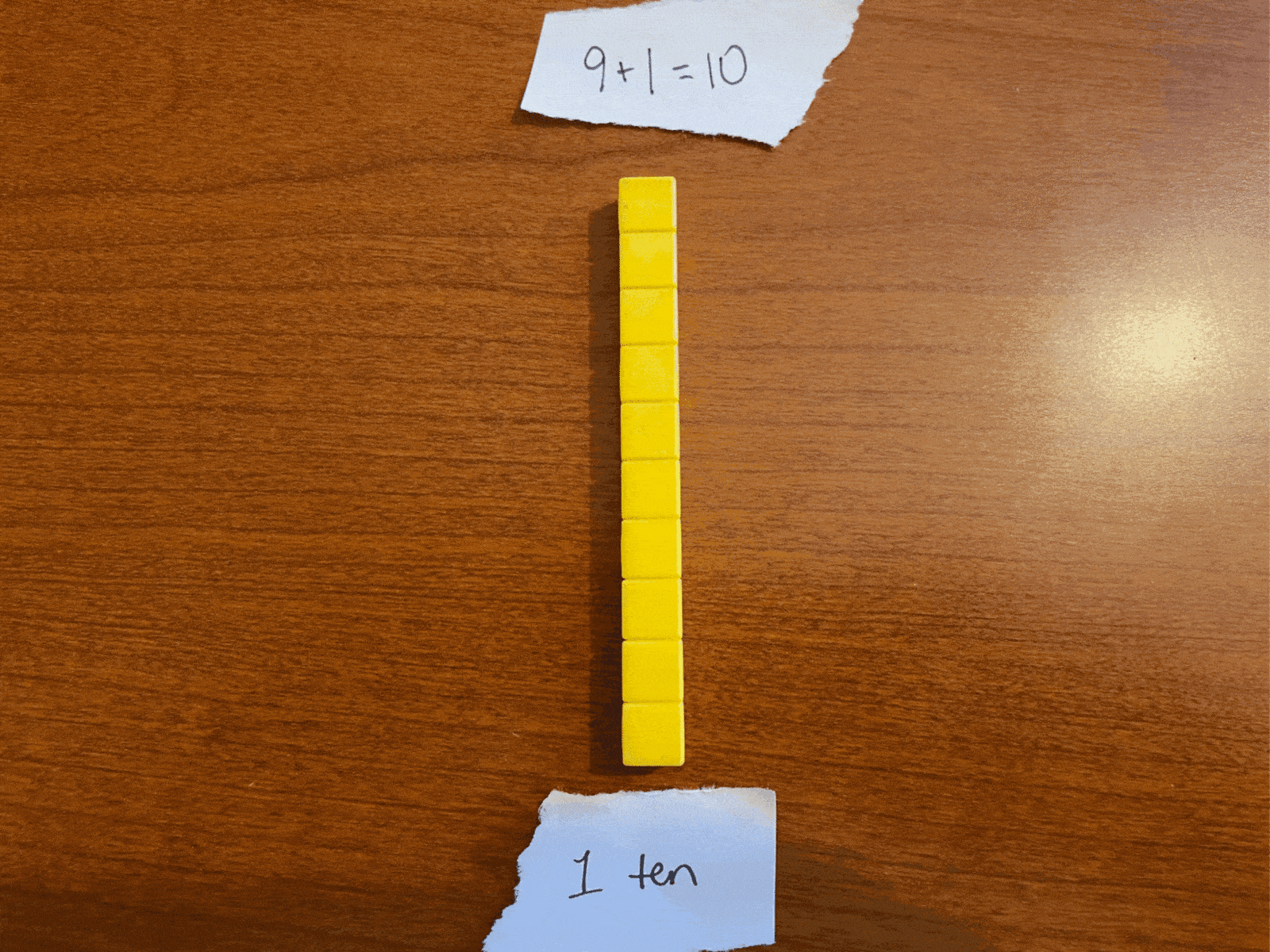
Similarly, the number 19 represents “one ten group and nine ones.” Adding 1 to this (19+1) makes “one ten group and ten ones.” but we can’t easily represent “ten ones” in that ones space.

So, instead, we group the ten ones together into a second group of 10 and call the new number 20 (written literally as “2-tens-and-no-ones”). Try saying two-tens as many times as fast as you can and see if eventually you don’t end up saying something that sounds kind of like “twenty” in the process.
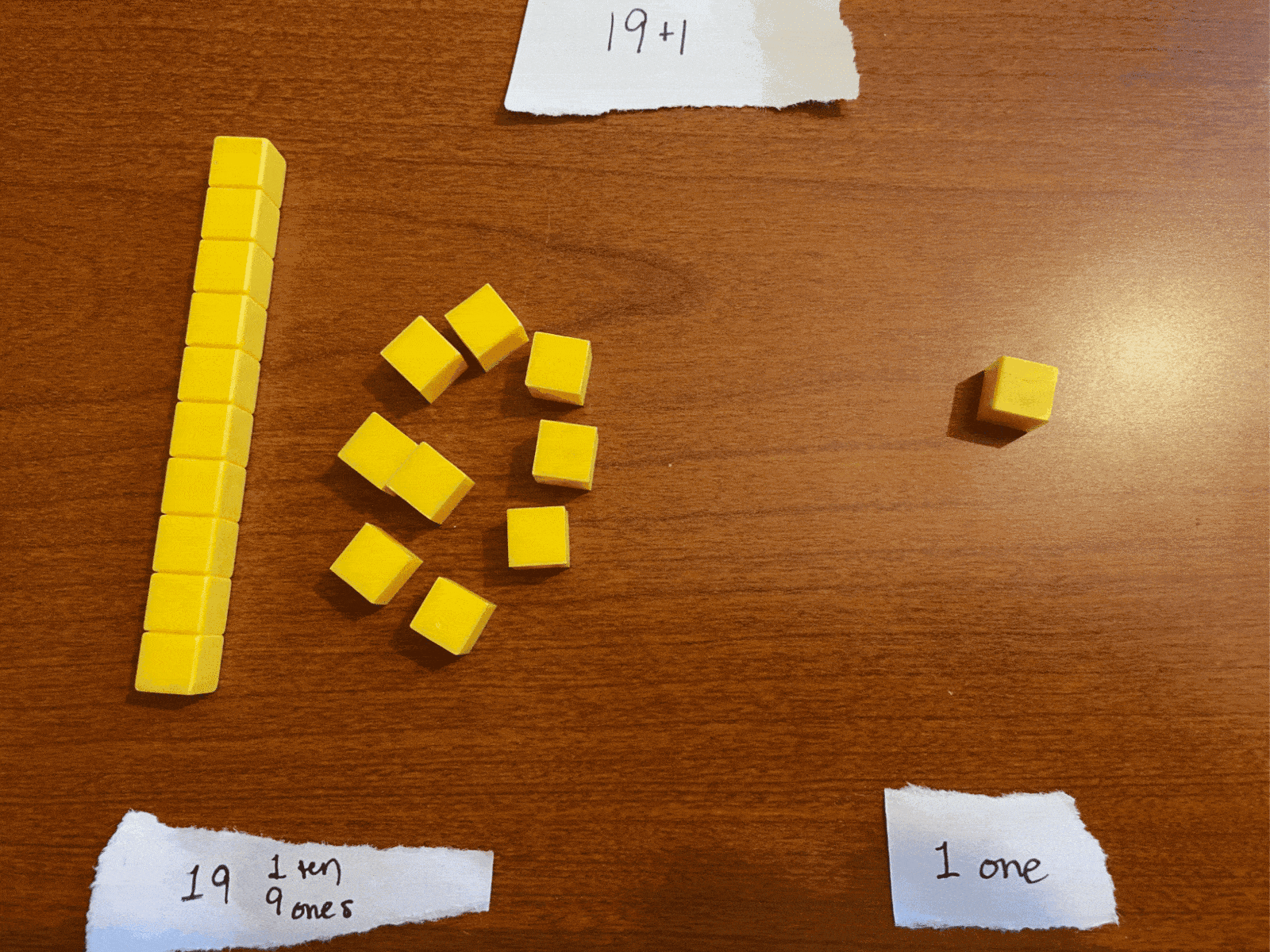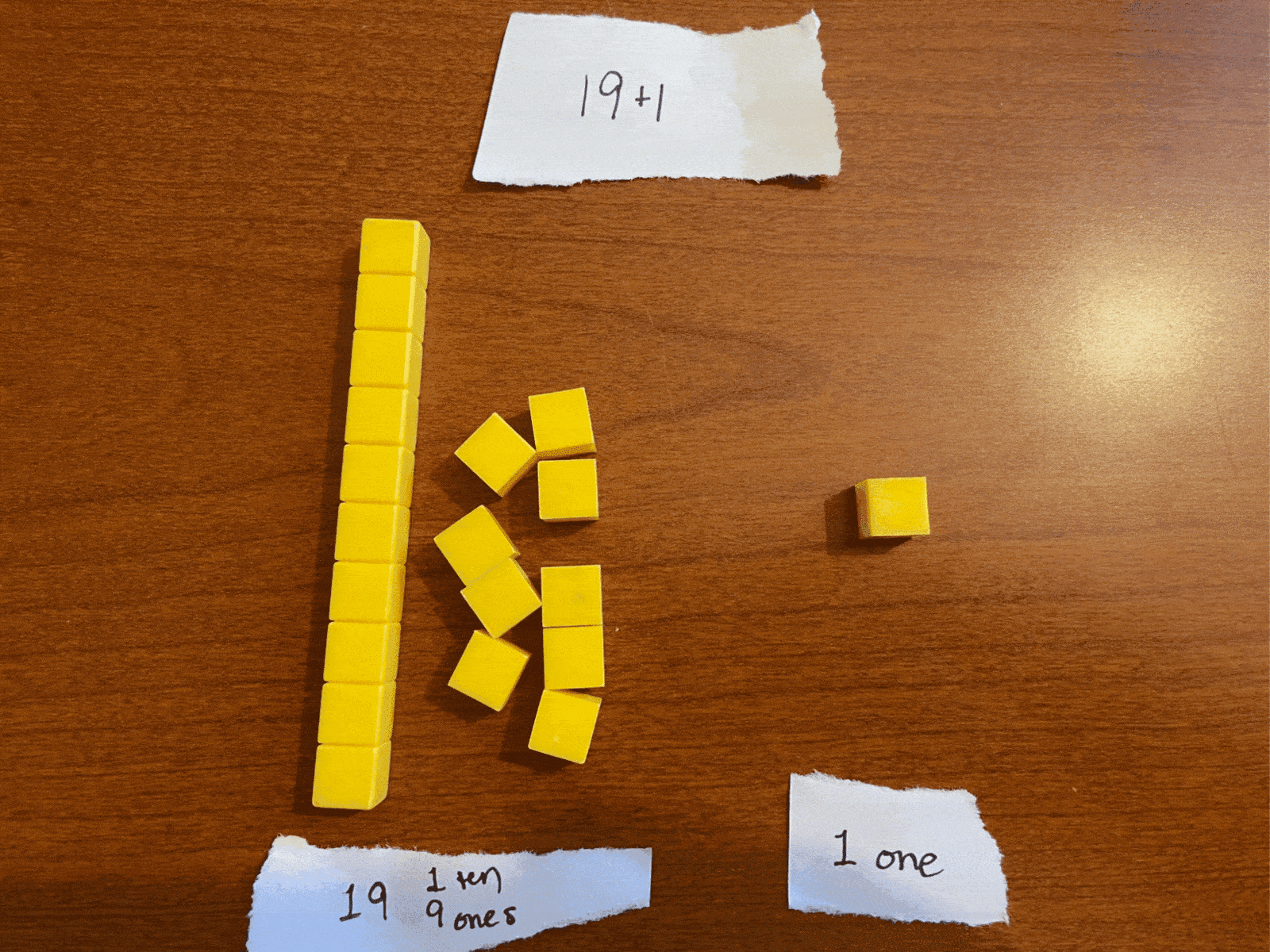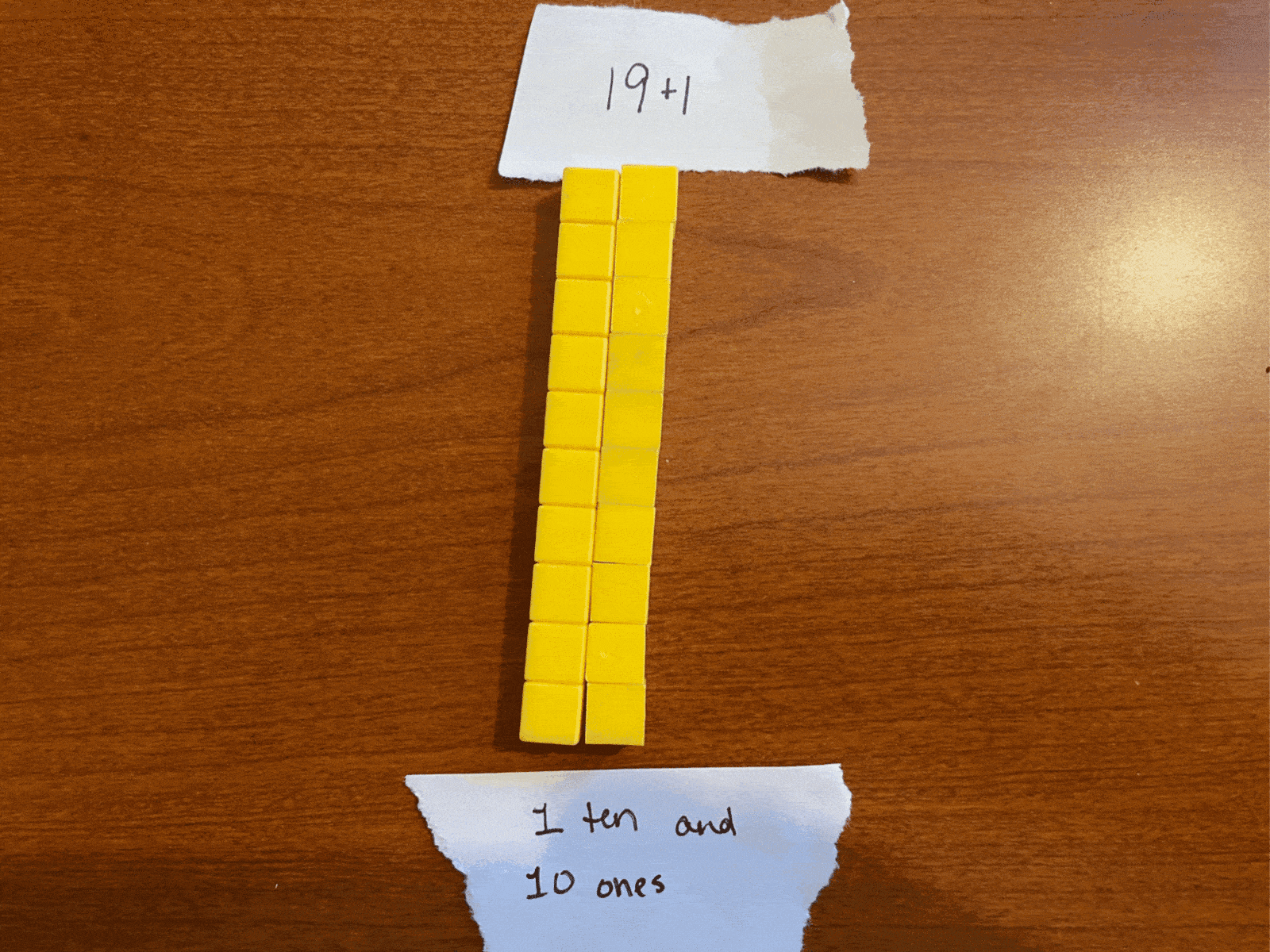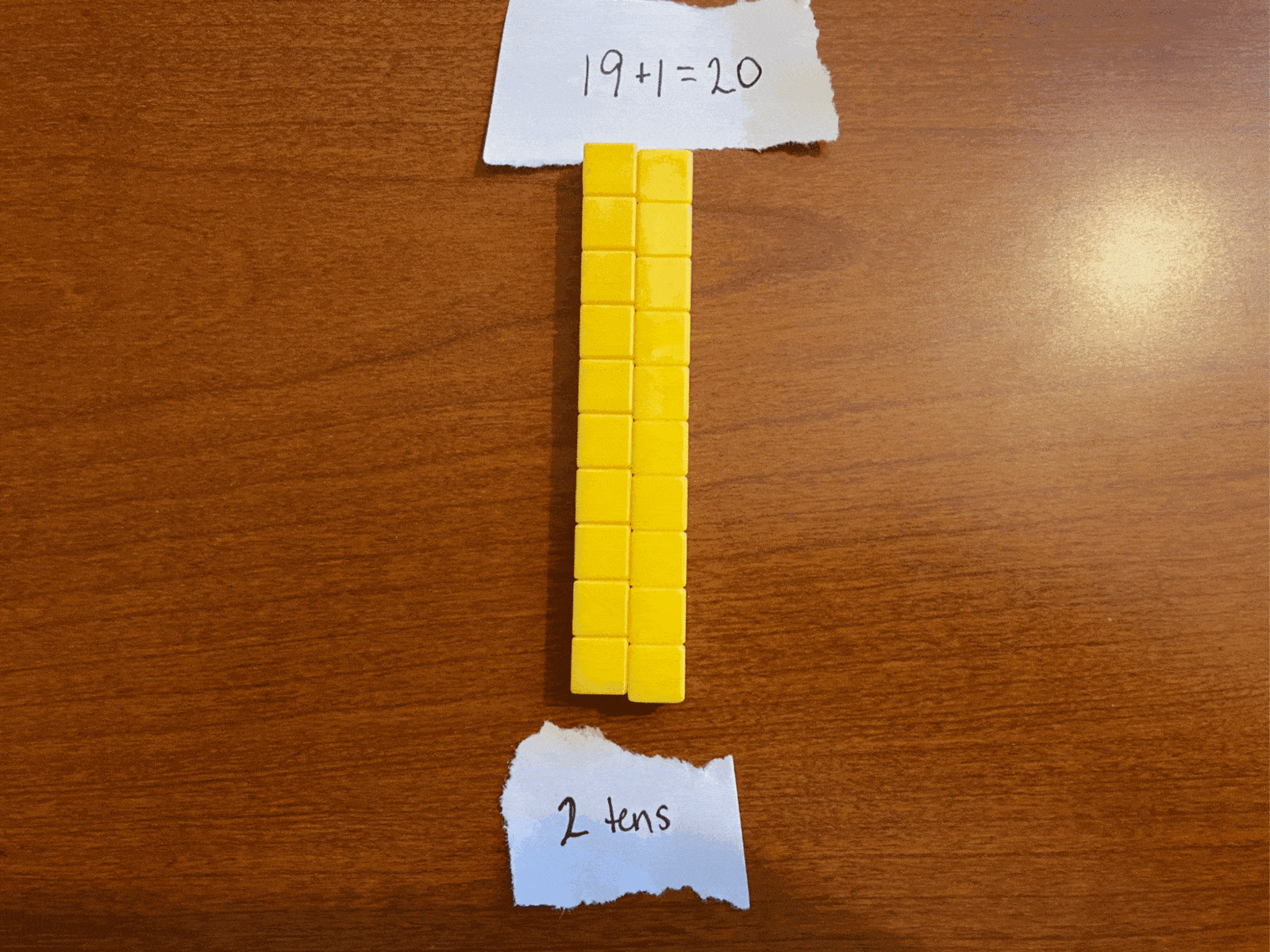
The same idea comes up when we try to add one to 99: 99+1. Can you picture this new number?
We don’t have a very good way to write “9 tens and 10 ones.” Like before, we could group the 10 ones into a “ten” group and have a total of “10 tens and no ones leftover.”
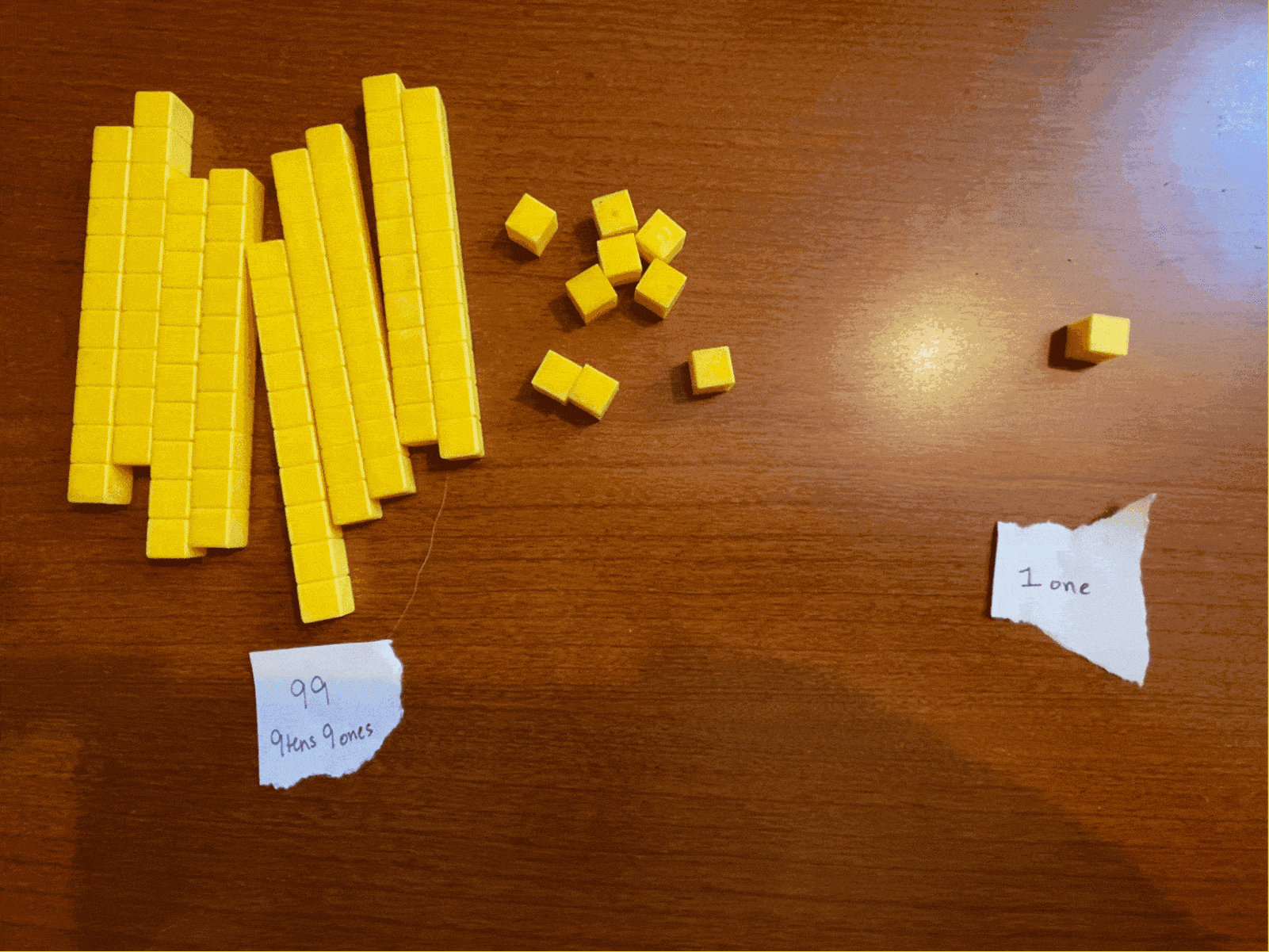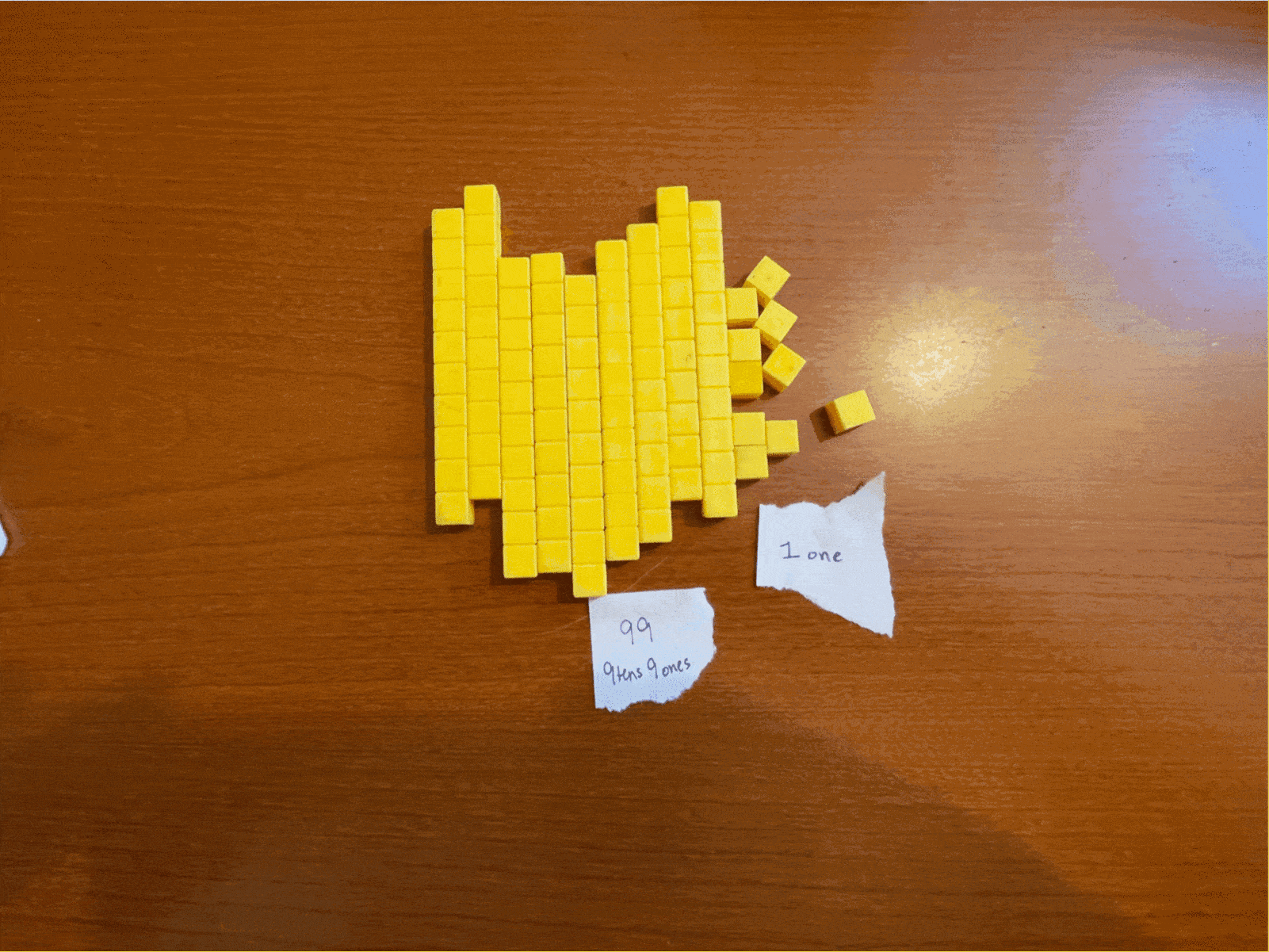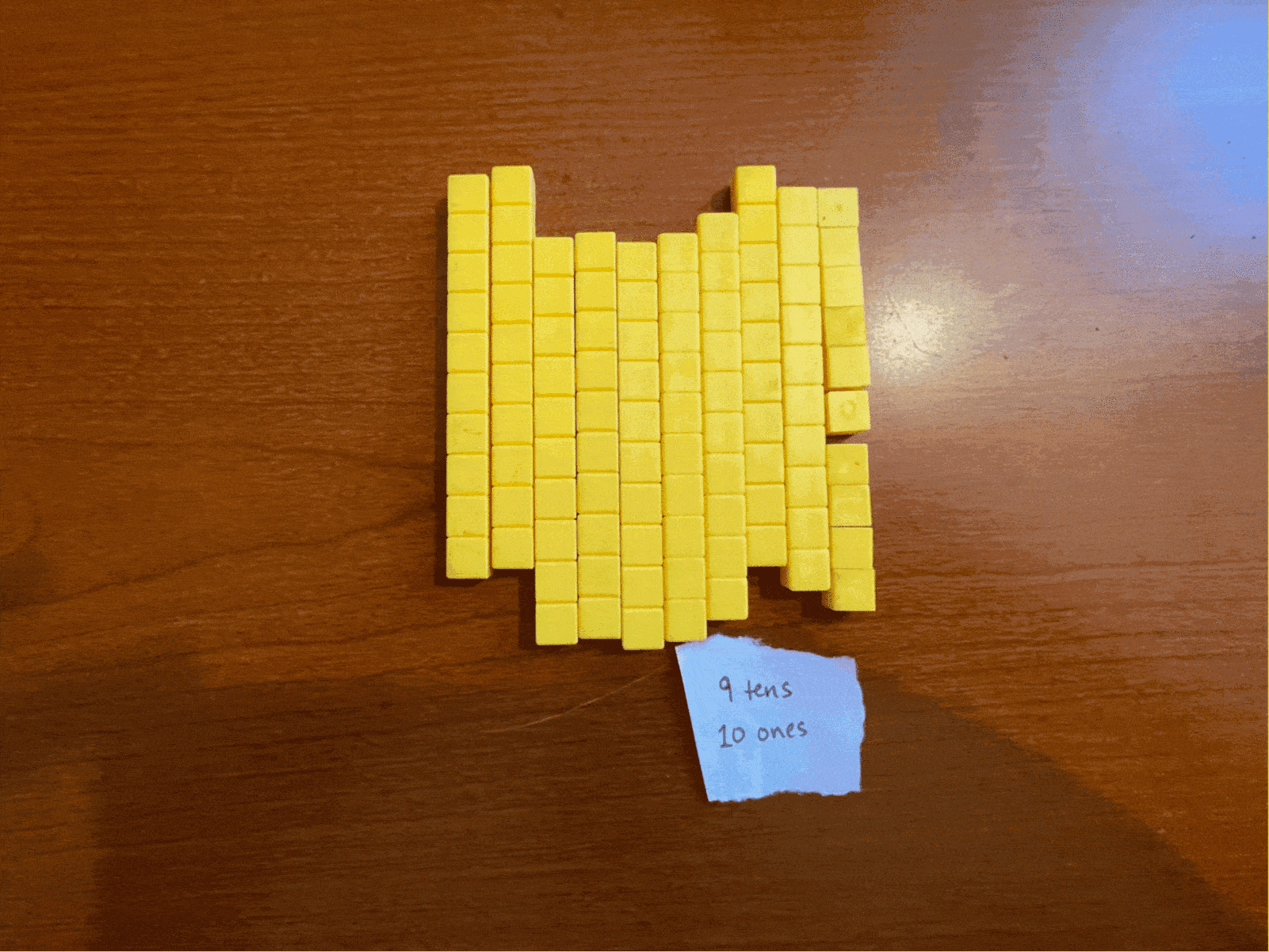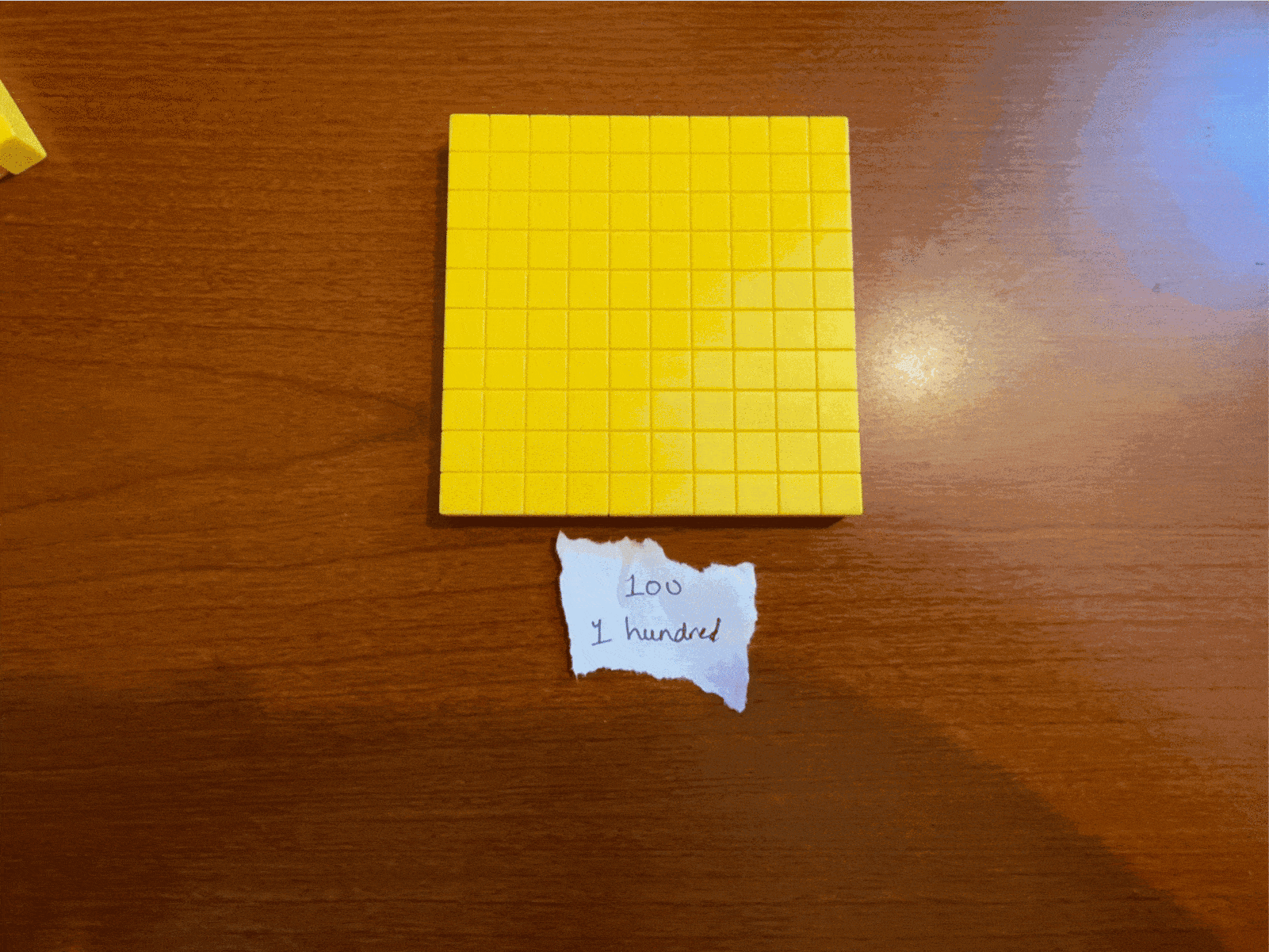
So we could write this as 100. We could possibly read this as “ten ones” without being contradictory. In fact, we do this all the time, both properly and improperly:
10,000 is read “10 thousand,” either a 10 in the thousands place or a 1 in the tenthousands place
1,400 is properly read as “1 thousand, 4 hundred” but we often shortcut that to “fourteen hundred” (a fourteen in the hundreds place)
For a deeper dive into how this idea of grouping (including carrying the one) is found all throughout math, from the very basics of counting and the number system itself, check out my post Grouping and Regrouping in Math.
Carrying the one: adding 1 in other place values
Now think about 99+10, or adding 1 ten to “9 tens and 9 ones.” So now we have a total of “10 tens and 9 ones.” This did not change how many ones we have! However, we have to either 1) figure out how to write a 10 in the tens place or 2) use a new place value to the left of the tens place.
In general, we’ll find that option 2 is almost always a safer bet. Option 1 is not reliable for most numbers. Do not choose option 1 in general. In this case, though, we can use option 1 to illustrate this idea of carrying the one:
- Write a 10 in the tens place and a 9 in the ones place: 109
- Use a new place value to the left of the tens place: 10 tens can group together to be 1 hundred. So we have “1 hundred, no leftover 10s, and 9 ones,” or 109.
Carrying the one vs regrouping
I’ve used the word “group” a lot so far, especially in the form of “group together” or “group into.” That was intentional and leads us into a short conversation about this idea of the language change that has happened for this activity. I won’t go too deep here, but if you want to know more, check out my post Regrouping, Carrying, Borrowing: Why the Vocabulary Changed.
In short, carrying the one is one version of regrouping. Regrouping refers to relating parts to the whole. Think of the idea that part+part=whole (or part+part+part=whole, or part+part+part+part=whole, etc). At its very core, regrouping refers to the ability to mix up the different ways parts can combine to make the same whole.
Carrying the one is not gone. You and your child will still learn to carry the one. But today we teach and recognize it for what it is: part of a larger phenomenon of regrouping at the very heart of math because it’s at the very heart of our number system.
For example, your child will do a lot of practice in school of the different ways to group 10 units. It may not be called regrouping at this stage, but it’s all part of the same phenomenon. In one problem, they may be called upon to see a group of 10 as 2 ones plus 8 ones, or 2+8=10. In another problem, 10 again will be grouped differently as 5+5. Or as 8+2. They may even be asked to regroup the same group of 10 items into different parts. (This is something you can make sure they have practice with! Set out 10 items and ask them to make as many different groupings of those items as they can and count the items in each grouping.) This is intended to build a fluency with the parts that can make up 10, smoothing their path when learning to add larger numbers later.

Carrying the one: adding other numbers
This leads us to the final point: we use carrying the one as a shortcut notation for regrouping when doing addition. When we add a column (a place value), sometimes we end up with too many items to fit the total count in that place value. In that case, we regroup 10 of those numbers (or sometimes 20 or 30 if we’re adding lots of numbers together) into groups of the next highest place value.
But they don’t go away when we regroup them. We have to remember to account for them in that next highest place value. So we jot a little note to ourselves above that next place value to remind us how many “extra” of that value we created in the step before. It’s a memory aid as well as a way to show our work (see this post for more on why that’s important). It’s not the only way, perhaps not even the most intuitive or meaningful way, but it’s a space-saving and sometimes time-saving way (this post talks more about how and why space- and time-saving were more important in previous generations while meaning-making takes precedence today).
Carrying the one is not gone. You and your child will still learn to carry the one. But today we teach and recognize it for what it is: part of a larger phenomenon of regrouping at the very heart of math because it’s at the very heart of our number system. Work alongside your child and watch for this principle of regrouping at work. Carrying the one is only one small means of using and notating regrouping. Can you find others ways your child and their teacher use and notate this idea?
You’ve Got This!
