How to Factor Numbers

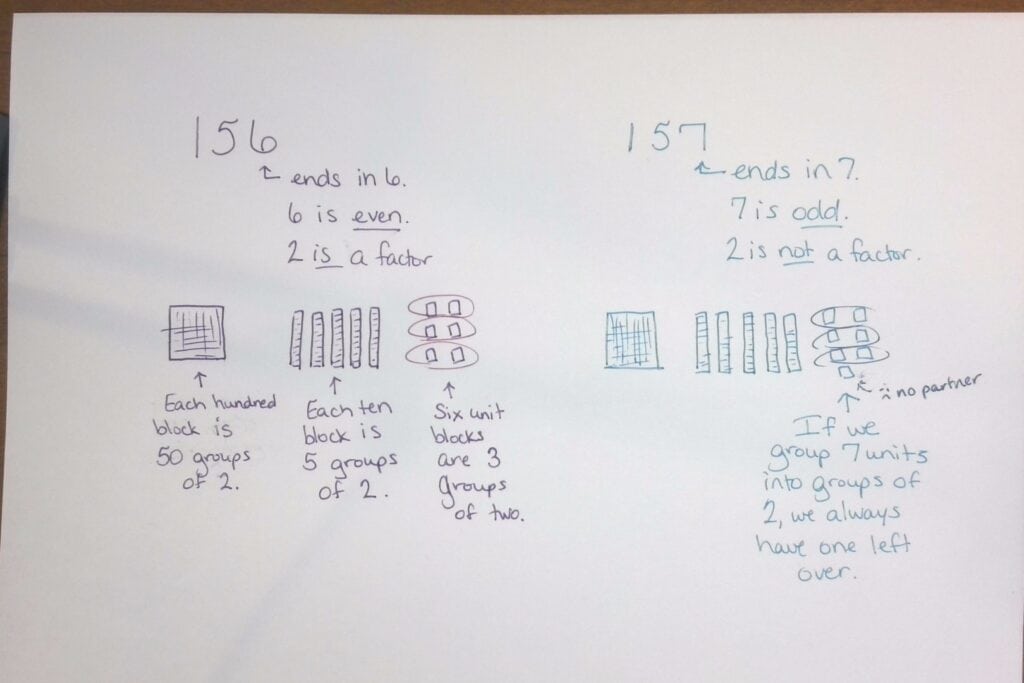
Shortly after we start multiplying, we’re taught to factor numbers. So often it feels like a pointless rite of passage that we’re forced to endure. We learn it devoid of all the contexts it will be useful in the future. We learn algorithms and strategies that feel prescriptive and scripted but really are anything but. Which is confusing. You want me to do it this way, but I get to start wherever I want? It feels like a contradiction and like we must be misunderstanding something.

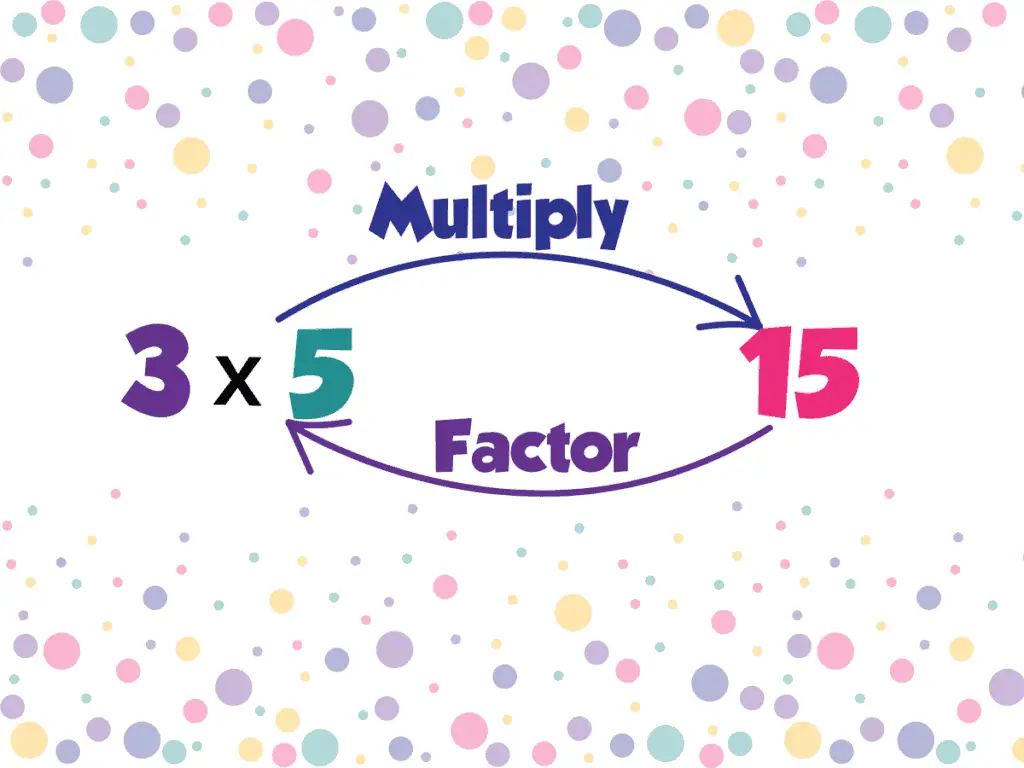
Factoring is the act of unmultiplying: finding the numbers (or in algebra, the expressions) that could be multiplied together to get the number we’re asked to factor. If we’re simply asked to factor a number, any collection of numbers (or expressions) that, when multiplied, make the number is a legitimate answer. If we want a more specific factoring, we have to look for an adjective or other information, such as prime factors or list of factor pairs.

Step 0: Know your basic multiplication facts

Factoring is just one of many math topics where any weaknesses in multiplication facts will slow you down. I have worked with many, many people who have struggled with math, and the vast majority of them would have had a better experience if they had known the multiplication facts enough to start becoming automatic. Practice factoring can be one piece of helping them become automatic, but it should only be one small piece. Knowing the facts separately and fluently will make first factoring, and then many, many, many other math topics much more accessible. If you need more research-backed ideas how to increase multiplication fluency, check out my post How to Learn Multiplication Facts: A Roundup.

Step 1: Know what “factor” means

noun: A factor of a certain Number is the same or different number that evenly divides the given Number.

verb: To factor a certain Number means to find pairs or groups of numbers that multiply together to make the given Number.

You might notice that I had to resort to capitalizing that word “Number” vs “number” in the above definitions in order to hold any hope of knowing which was which. Perhaps some official math terminology will help.

In math, a multiplication problem has the following parts: factor $\times$ factor $=$ product.

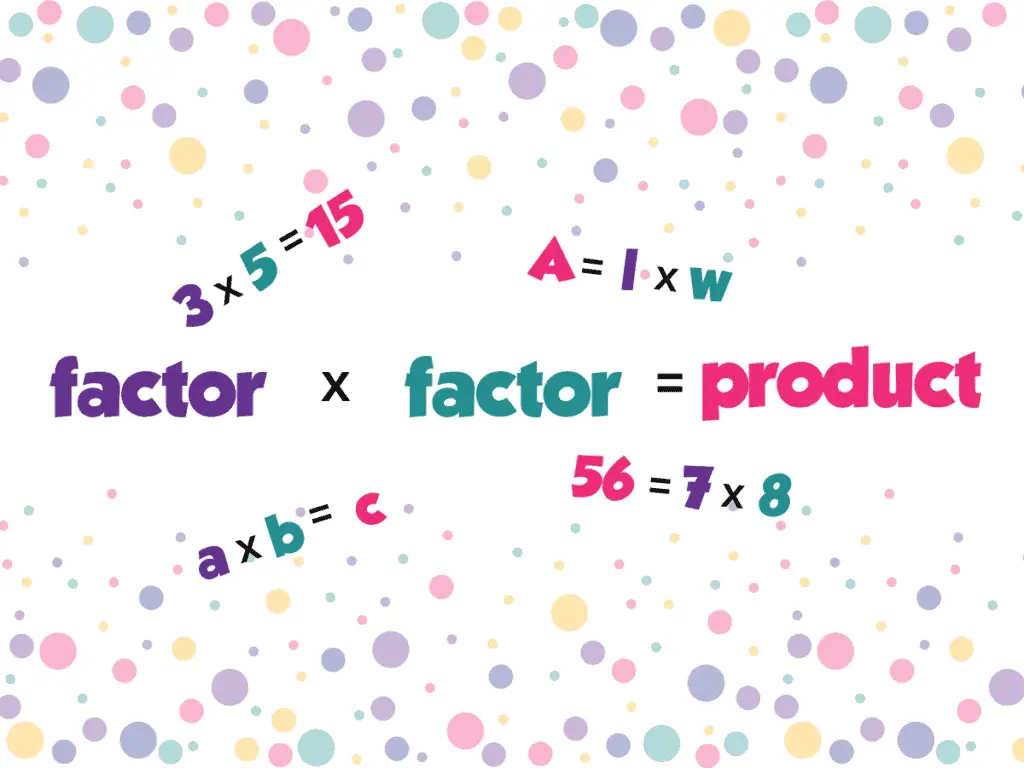
The product is the result of multiplying — the “answer” of a multiplication problem, if you will. The factors are the numbers that are being multiplied together. So, using these terms in our definitions:

noun: A factor is a number that evenly divides the given product.

verb: To factor is to find pairs or groups of factors (see noun above) that equal the product when multiplied together.

When we are asked to factor a number, we are asked to find numbers that could and would multiply together to make that original number.

With this understanding, is it becoming obvious why it’s important to know your multiplication facts well? We’re about to use them “backwards”. It’s hard to turn any knowledge backward and inside out if we don’t know it really, really well.

Step 2: Find one factor

I’ll talk more specifically about different variations and directions below. But for all of them, let’s start by finding just one factor of the given number. Even if it’s a factor we don’t use in our final answer (it’s rare not to), it tells us something about the number. There are two main ways to find this first factor. Pick the one that works for you and for the number you’re factoring:

• If you know a multiplication fact with the number as a result, such as 12 ($3 \times 4=12$ or $2 \times 6=12$, then bonus! You’ve just found a factor pair, not just a single factor, and have completed multiple steps at once! In the example of 12, you could use either factor pair, whichever you think of first or whichever is your favorite:
  • 3 and 4 are factors of 12
  • 2 and 6 are factors of 12
• If the number is not part of the multiplication tables you know well, then you can perform divisibility tests to find out what numbers are factors.

Divisibility Tests, also called Divisibility Rules

A common strategy is starting small and building up to bigger numbers until you find one that divides the given number evenly. It is usually efficient to test only prime numbers (the ones on the following list), with one exception that I’ll list first because it’s the easiest:

There are similar divisibility rules for larger numbers, but they get more and more complicated (you can see this already starting to happen with the 7s and 11s). Most textbooks and teachers find the 11s rule a convenient place to stop teaching the divisibility rules. To test larger numbers, use your favorite division method to find out if it divides without remainders. (An advantage of using a division method to find out is that you end up with a factor pair, not just a single factor!)

*This rule is relatively new to the common population. When I was a kid, we just had to divide and see if it came out with or without remainders!

Step 3: Know the specifics of the question being asked

Now that you know one factor (or maybe two), it’s time to read the question again to make sure you know what your answer should look like. Are you being asked to “find a factor pair,” “list the factor pairs,” “is ___ a factor of ____,” or “find the prime factors of”? (There may be other variations I’m not thinking of right now. I’ll add them as they come up.) The next step depends on the specific question being asked.

Step 4: Find the paired factor

So in Step 2, you found one factor. If you used a method that found a factor pair (such as knowing it as a multiplication fact or using direct division), then congratulations! You’ve already completed this step and can move onto the next one.

If, however, you used a divisibility rule to find the first factor, you’ll need to do some division to find the other, paired factor. Divide your original number by the factor you found. The result will be the paired factor.

Example: Find a factor pair of 4,070.

Solution: We determined that 11 is a factor of 4,070. So now we need the paired factor. Divide 4,070 by 11:

[image here]

Since $4070 \div 11=370$, a factor pair of 4,070 is 11 and 370.

If the question only asked you to find a factored pair, then you can skip to step 7!

Step 5: Repeat until all factors are found

The question might ask you to “find all factor pairs” or to “list all the factors” or something similar. In that case, we will need to repeat the above steps until we find all of them. If you approach this methodically and organized, it can be a lot easier to make sure you’ve found them all.

We’ll use the rules from Step 2 above, but we’ll also add some rules for composite (not prime numbers — namely, the ones we skipped). The most common way to do this is to go through the divisibility rules from smallest to largest factors. Let’s go through and example step-by-step. We’ll factor 1,100.

• Is it divisible by 2? 1,100 is even, it can be halved, and it ends in 0. So, yes, it’s divisible by 2. If we divide it in half to find the paired factor using your favorite division algorithm. I like to do this in my head by thinking of $1100=1000+100$ and halving each part. Half of 1000 is 500. Half of 100 is 50. So half of 1,100 is $500+50=550$. One factor pair is 2 and 550.
• Is it divisible by 3? I add the digits: $1+1+0+0=2$. The result is small enough but is not on the 3s times table, so 1,100 is not divisible by 3.
• Is it divisible by 4? If it’s not divisible by 2, then it’s not divisible by 4. But our example is divisible by 2, so it might be divisible by 4. Find the paired factor that goes with the 2. Is that paired factor also divisible by 2? Then this number is divisible by 4. The paired factor to 2 is 550. 550 is still divisible by 2, so let’s do that division: $550 \div2 = (500+50) \div 2 = 250+25=275$. One factor pair is 4 and 275.
• Is it divisible by 5? 1,100 ends in a 0, so yes, it’s divisible by 5. Divide it out your favorite way. I can do something similar to what I did for the 2s, or I can use long division or any other favorite algorithm. $1100 \div 5=(1000+100) \div 5 = 200+20=220$. One factor pair is 5 and 220.
• Is it divisible by 6? Since $6=2\times 3$, the number has to be divisible by both 2 and 3 to be divisible by 6. 1,100 is not divisible by 3, so it’s also not divisible by 6.
• Is it divisible by 7? This was the weird rule, and you might actually prefer just to divide it directly. But here let’s practice the rule. The last digit of 1,100 is 0. Double that: $0\times 2 =0$. Subtract the result from the other digits as if they were a number by themselves: $110-0=110$. Is it on the 7s table? Well, it’s bigger than what most of us memorize to, so let’s repeat. The last digit of 110 is 0. Double that: $0\times 2 = 0$. Subtract the results from the other digits: $11-0=11$. 11 is not on the 7s table, so 1,100 is not divisible by 7.
• Is it divisible by 8? One way we can think of multiplying by 8 is as a “double-double-double” since $8=2\times 2\times 2$. So to divide by 8, we could think of it as “halve-halve-halve”. Look at your 4 factor pair. If we can halve that factor paired with 4 one more time, then the number is divisible by 8. We found that $1100=4\times 275$. But 275 is odd and not divisible by 2. So 1,100 is not divisible by 8.
• Is it divisible by 9? Since $9=3\times 3$, if a number is not divisible by 3, then it is also not divisible by 9. (If it is divisible by 3, then you have to compare the paired factor and find out if it’s also divisible by 3, similar to the test for 4 except using the 3-rule instead of the 2-rule.) Since 1,100 was not divisible by 3, then it also isn’t divisible by 9.
• Is it divisible by 10? 1,100 ends in a zero, so it’s divisible by 10! $1100=10*110$, so a factor pair is 10 and 110.
• Is it divisible by 11? Remember the 11 rule had us adding together every other digit and subtracting the odds-placed digits and evens-placed digits. In 1,100, this looks like $1+0=1$ and $1+0=1$, then subtracting $1-1=0$. The result is 0 (or a multiple of 11), so 11 is a factor. We divide in order to find out what the paired factor is. Use your favorite division algorithm. Or think of the short-hand version of how many of us casually pronounce that number: “eleven hundred.” That casual pronunciation is not wrong, it’s just casual (which is why some teachers will count it as wrong). Anyway, that language makes it clear that 1,100 is 11 hundreds, or $1100=11\times 100$. So one factor pair is 11 and 100.

Now here’s where things get a bit tedious for these bigger numbers. We’ve run out of divisibility rules. But there are potentially a lot of numbers left to check. Let’s think about the list of the next 21 numbers: 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32. Can we rule any out?

• 12: $12=3\times 4$. But 1,100 is not divisible by 3, so it also won’t be divisible by 12. In fact, every multiple of three will be ruled out for this reason.
• We don’t need to check 12, 15, 18, 21, 24, 27, or 30 because they’re multiples of 3.

12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32

• 1,100 was also not divisible by 7, which knocks out all the numbers on the 7s table as well. In this case, eliminating 14 and 28 (21 was already eliminated).

12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32

• Similar for 8: 1,100 was not divisible by 8, and 16 and 32 are on the 8s table, so they are also eliminated.

12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32

We’ve now cut our list in half. We do need to test these, which will involve some division. But at least it’s not a lot of division problems.

• Divisible by 13? $1100\div 13 = 84 R 8$, so 13 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 17? $1100\div 17=64 R12$, so 17 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 19? $1100\div 19=57 R17$, so 19 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 20? $1100\div 20=55$ with no remainder, so 20 and 55 are a factor pair.
• Divisible by 22? $1100\div 22=50$ with no remainder, so 22 and 50 are a factor pair.
• Divisible by 23? $1100\div 23=47 R19$, so 23 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 25? $1100\div 25=44$ with no remainder, so 25 and 44 are a factor pair.
• Divisible by 26? $1100\div 26=42 R8$, so 26 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 29? $1100\div 29=37 R27$, so 29 does not divide 1,100 evenly, and thus is not a factor.
• Divisible by 31? $1100\div 31=35 R15$, so 31 does not divide 1,100 evenly, and thus is not a factor.

Important note: this process can be shorter with a good understanding of prime factorization! For example, if we found the prime factorization of 1,100 ($1100=2\times 2\times 5\times 5\times 11$), we would know right away that no other prime numbers can be factors, thus eliminating 13, 17, 19, 23, 29, and 31 right away (as well as 26 from its being $2\times 13$). But that’s a topic for a different blog post (such as this one giving the example of factoring the number 72.)

Step 6: Make sure you’ve found them all

Did you go through the list methodically in order, without skipping any number tests? I know it’s tedious and boring, but it’s the best way to make sure you don’t miss any.

Assuming you did, how do you know when you can stop? Doing every number between 1 and 1,100 seems unreasonable.

Well, have you noticed that the factors in each factor pair get closer and closer together? At some point, you end up with the first number starting to be bigger than the second number. When this happens, you’ll be repeating the same factor pairs over but in reverse order. That tells you that you’ve finished.

For our example, consider 33. Since 33 is on the 3s table, we know it won’t be a factor, but what does happen when we divide $1100 \div 33$?

$1100 \div 33=33 R11$

Ignoring the remainder for just a moment, do you see how this is the turning point for the factors to flip roles? The tested number is approximately the same size as the result of the division. This tells us we’re done.

Step 7: State your answer clearly, visibly, and directly.

In our example of 1,100…

The factor pairs of 1,100 are 2 and 550, 4 and 275, 5 and 220, 10 and 110, 11 and 100, 20 and 55, 22 and 50, 25 and 44

The factors of 1,100 are 2, 4, 5, 10, 11, 20, 22, 25, 44, 50, 55, 100, 110, 220, 275, and 550.

You’ll notice that I almost always list this, or something similar, as the final step. I can not underemphasize the importance of this. Individual teachers may have specific ways they ask you to do this, but this is the point each time. There are multiple reasons for stating your answer clearly, visibly, and directly:

• It helps you know that you answered the actual question that was asked and not some other question that distracted you along the way.
• It sometimes helps you do a quick check for appropriateness. If you end up writing an illogical sentence (such as one person buying 1,021 watermelons), you might notice the absurdity and rethink the problem before it is graded.
• It helps your teacher spot your answer. They have a lot of work to review, grade, as well as prepare. So anything to help them be more efficient is a good thing.
• It helps you stay organized even if you weren’t organized in the middle.
• It helps you move the process into long-term memory as writing up the solution requires a small amount of reviewing what you did and what the goals were.
• And perhaps most importantly: It builds good habits of effective communication. Skills that are useful in all areas of life, not just math class.

You’ve Got This!