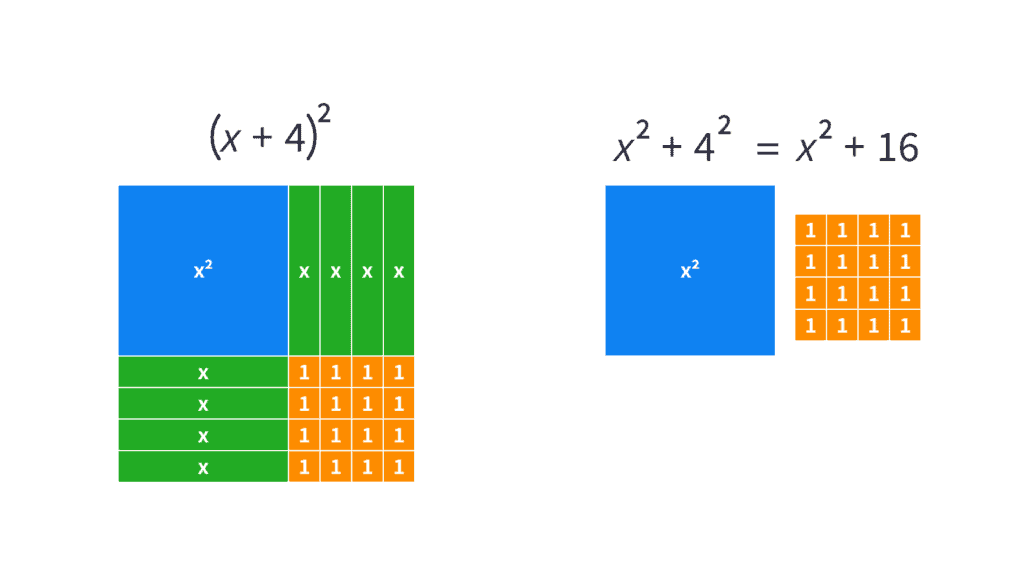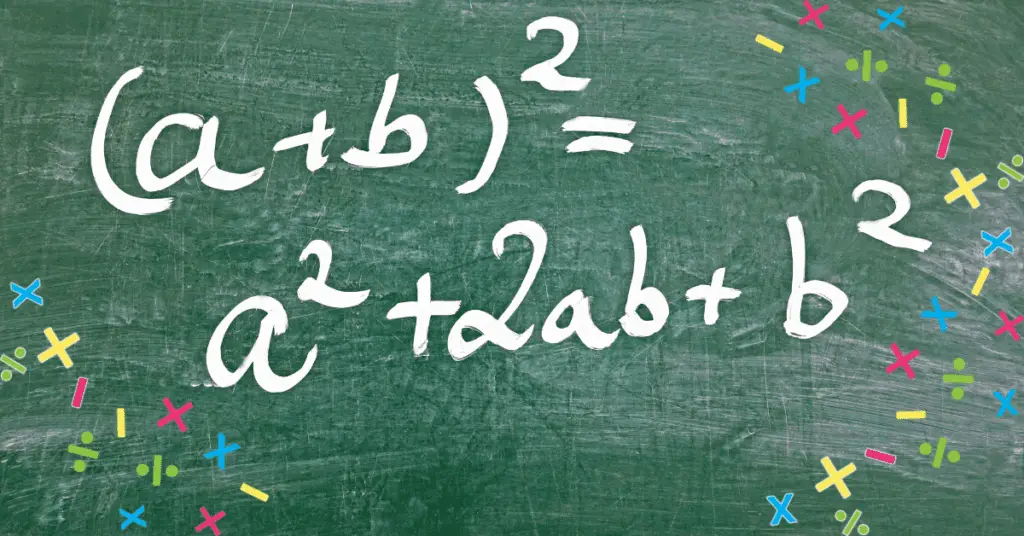
It’s tempting to think that squaring a binomial means simply squaring each term. I mean, if math is logical and makes sense, it should be that easy, right? Yet, algebra students (and even students well beyond algebra!) have this marked wrong every day. In reverse, we learn to factor the difference of squares (though again never quite as straightforward as we wish!), but we’re told that the sum of two squares can not be factored.
Squaring any polynomial properly requires either writing out each factor and repeatedly using the distributive property of multiplication across division, or memorizing the patterns resulting from doing this. The square of the sum is not equal to the sum of the squares.
This post contains affiliate links. If you purchase through these links, I may earn a small commission at no additional cost to you. You can read more about how I choose affiliates and products at my affiliate page.
Here are seven reasons why simply squaring out $(x+4)^2$ does not give us simply the sum of the squares $x^2+16$.
1. (Symbolic) Expand the exponent and multiply the factors
We’ll start with most algebra teachers’ and textbooks’ default explanation (at least in my experience). What does it mean to square a number (or expression)? Most often we think about exponents as repeated multiplication. So, if this is what exponents mean, then $( )^2$ must be $( )*( )$ for whatever is in the parentheses. In this case, $(x+4)^2=(x+4)(x+4)$. When we see $(x+4)^2$ our brains really want to shortcut the problem and square each term inside. But when we look at $(x+4)(x+4)$ our brains don’t do that. Our muscle memory takes over and we double-distribute (you may have learned this as FOILing). So,
$(x+4)^2=(x+4)(x+4)=x^2+4x+4x+16=x^2+8x+16$.
Notice this does not equal $x^2+16$. In fact, it’s different by $8x$.
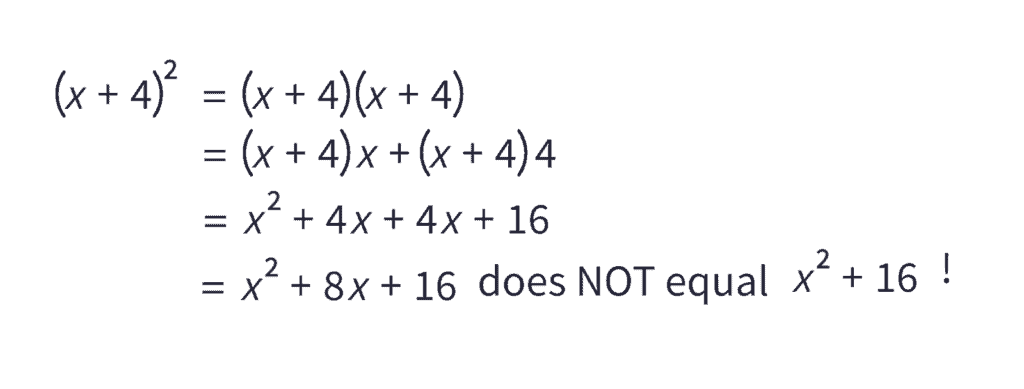
2. (Symbolic) Factor $x^2+16$
The conversation about sums of squares and squares of sums typically comes up twice in an algebra classroom (then quietly student-by-student as the error continues to be made). The first time when students are learning to multiply polynomials, and the second time when they are learning to factor them. So let’s try to factor this binomial, but without using “shortcuts,” “tricks,” or memorized “special patterns.” (If you need a quick review of factoring in algebra, I have a YouTube playlist for that.)
If we pretend to be a computer that has been programmed with our factoring algorithms, we would be looking for 1) common factors and 2) three or four terms written in descending degrees. Since $x^2=x \dot x$ and $16 = 2 \dot 2 \dot 2 \dot 2$, there are no common factors between the terms. So let’s make all the descending terms visible, and rewrite this as $x^2+16=x^2+0x+16$ with the 0x middle term, previously unnecessary to write, made visible. So we look for two factors of 16 that add up to be zero! Hm… let’s see… $1+16=17$… $2+8=10$… 3 doesn’t divide 16… $4+4=8$… these are all the positive factor pairs of 16. None of the negative factor pairs add to zero either! So we can’t find a factor pair that adds up to the coefficient of the middle term. When this is true, and when there are no common factors, we’ve been taught to call this polynomial prime. So $x^2+16$ is prime! This means it doesn’t factor. So it definitely can’t be two $(x+4)$ factors!
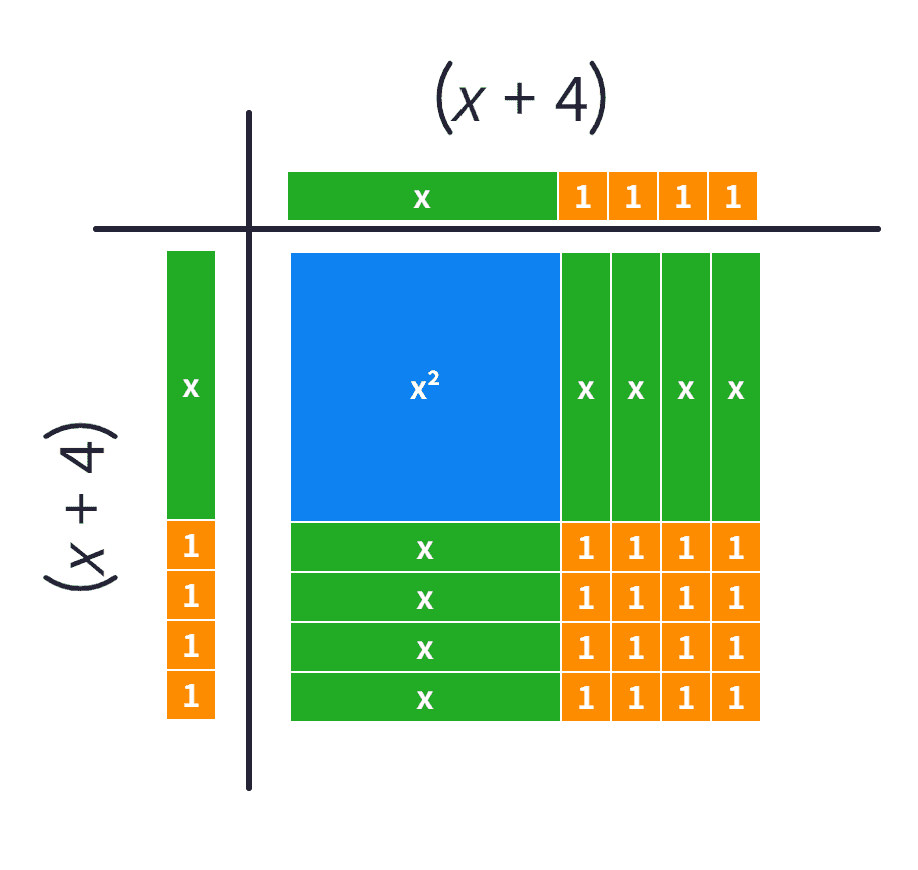
3. (Geometric) Multiplying with the area model (ie, Completing the Square)
The area model is a way of keeping track when multiplying that uses multiplication as the area of a rectangle. You can see how the area model is used with numbers in this blog post or this YouTube playlist. If you want more information about how to use the area model in algebra, let me know at this feedback form.
Notice in the images below that $x^2+16$ is only part of the square made up by $(x+4)^2$!
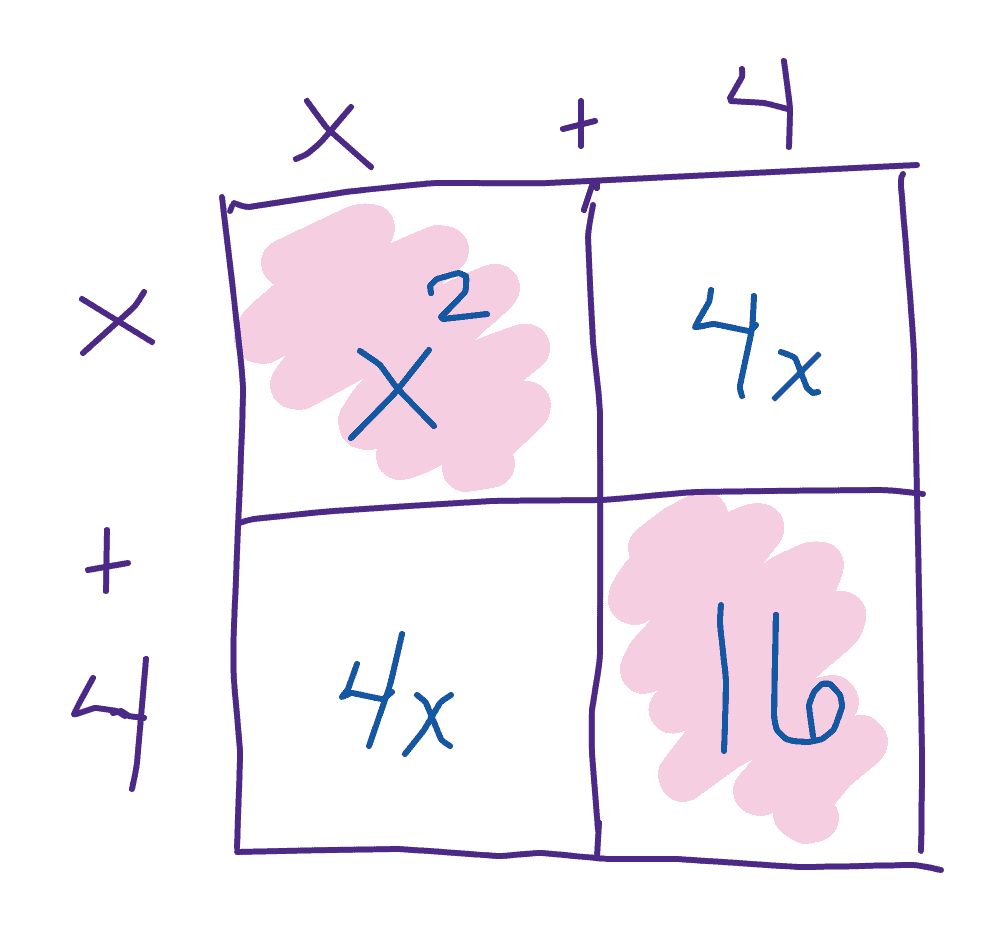
4. (Geometric) Algebra Tiles
Algebra tiles (affiliate link) are, at their core, a way to kinesthetically explore the area model above. Thus, this argument is not significantly different than the area model argument. However, if you are more familiar with algebra tiles, this may help you. (If you’d like to know more about using algebra tiles, check out my blog post introducing algebra tiles and what they stand for. If you want some great, free, virtual tiles, check out polypad.org.)
The first image shows algebra tiles set up as the result of multiplying $x+4$ times $x+4$, including the frame and the factors. The second image shows just the tiles that resulted from that multiplication on the left (ie, without the frame or the factors), and the tiles that represent $x^2+16$ on the right. It is clear to see, from the absence of the long thin $x$ rectangles on the right, that the two expressions are different.
5. (Numeric) Plugging in values and building a table
If two expressions are actually equal, then they are equal everywhere they are both defined. In other words, if I plug a value in for $x$ in one expression, I should get the same result I get plugging the same value of $x$ into the other expression. If they’re different anywhere, then the expressions are not equal. Let’s use this to see whether $(x+4)^2$ is or is not equal to $x^2+16$. (As you’re looking at the table, remember that a negative number squared makes a negative times a negative, which is always a positive.)
| $x$ | $(x+4)^2$ | $x^2+16$ | Equal or not? |
| $-3$ | $((-3)+4)^2=(1)^2=1$ | $(-3)^2+16=9+16=25$ | not equal |
| $-2$ | $((-2)+4)^2=(2)^2=4$ | $(-2)^2+16=4+16=20$ | not equal |
| $-1$ | $((-1)+4)^2=(3)^2=9$ | $(-1)^2+16=1+16=17$ | not equal |
| $0$ | $((0)+4)^2=(4)^2=16$ | $(0)^2+16=0+16=16$ | equal |
| $1$ | $((1)+4)^2=(5)^2=25$ | $(1)^2+16=1+16=17$ | not equal |
| $2$ | $((2)+4)^2=(6)^2=36$ | $(2)^2+16=4+16=20$ | not equal |
| $3$ | $((3)+4)^2=(7)^2=49$ | $(3)^2+16=9+16=25$ | not equal |
Notice that $(0+4)^2$ equals $0^2+16$, but none of the other lines are equal. So these expressions can not be equal to each other.
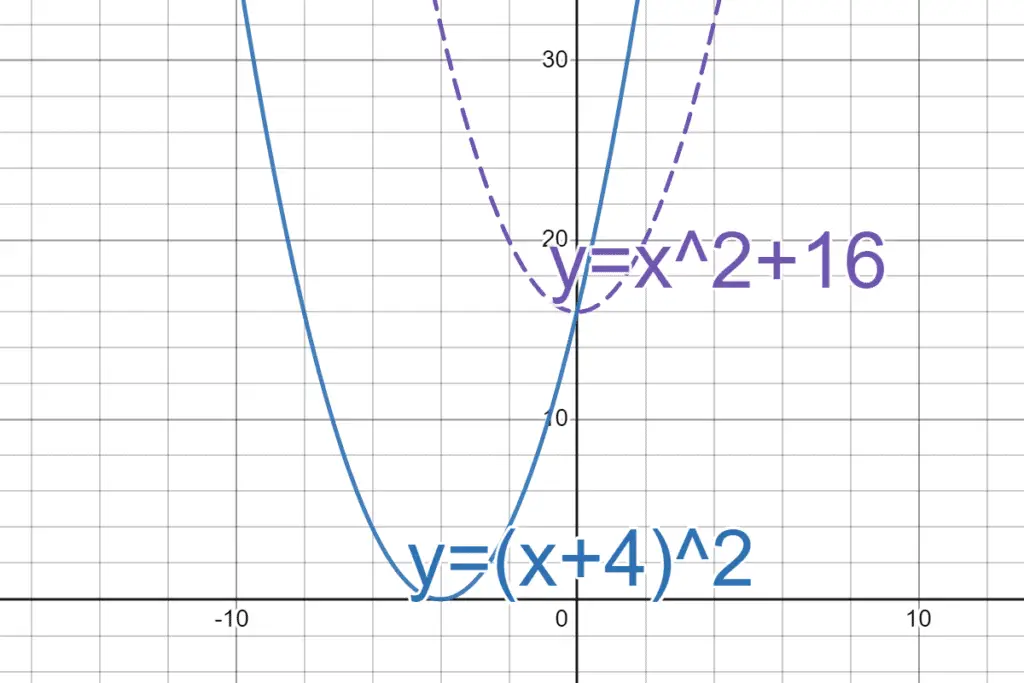
6. (Graphical) The graphs don’t match
If two expressions are equal, then their graphs should be the same when the (input,output) $(x,y)$ pairs are plotted on the coordinate plane. Let’s see what happens with $(x+4)^2$ and $x^2+16$:
Notice that the graph of $y=x^2+16$ (dashed, purple curve) is higher and to the right, while the graph of $y=(x+4)^2$ (blue, solid curve) is lower and to the left. Clearly, these are not the same graph, so they must not be equivalent expressions.
7. (Order of Operations) Distributive Properties
This argument is a bit non-traditional, but stick with me. Turns out: We can only distribute any operation across the operation directly below it in the Order of Operations list!
What we usually call the distributive property is really the distributive property of multiplication over (or across) addition. Notice that in multiplying $3(x-2)=3x-6$ we’re really multiplying by 3 across or over or through an addition problem.
When we learn about exponent properties, we learn that we can do something similar with exponents across multiplication. Our books and notes usually show this as $(ab)^n=a^n b^n$. We might even call this the distributive property of exponentiation over (or across) multiplication!
So we can distribute one operation across, or through, an operation immediately below it in the order of operations, but turns out (by all of the arguments #1-6) that we are not allowed to distribute by skipping through the order of operations (nor going backwards through). Food for thought!
Order of Operations
(Yes, I ignored the “grouping symbols” step to focus only on the actual operations.)
Exponents/roots
Multiplication/Division
Addition/Subtraction
I hope at least one of these arguments convinces you, sticks with you, and helps you save a few points the next time this comes up in a graded assignment.
You’ve Got This!
This article uses screenshots, images, and activities created using the tools at polypad.org by Mathigon at Amplify with permission. The graphs under reason number 6 are made with the Desmos graphing calculator. Use of Desmos Tools in videos is used with permission from Desmos Studio, PBC.